Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu nào cũng ghi lại đề nha
a) \(x\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
b)\(x\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
c) \(\left(x+1\right)\left(x+2\right)+\left(x+2\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+1+x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{2}\end{matrix}\right.\)
d) \(\dfrac{1}{x-2}+3-\dfrac{3-x}{x-2}=0\)
\(\Leftrightarrow\dfrac{1+3\left(x-2\right)-\left(3-x\right)}{x-2}=0\)
\(\Leftrightarrow\dfrac{1+3x-6-3+x}{x-2}=0\) ( đk \(x\ne2\) )
\(\Leftrightarrow4x-8=0\Rightarrow x=2\)
đ) \(\dfrac{8-x}{x-7}-8-\dfrac{1}{x-7}=0\)
\(\Leftrightarrow\dfrac{8-x-8\left(x-7\right)-1}{x-7}=0\) (đk \(x\ne7\))
\(\Leftrightarrow8-x-8x+56-1=0\)
\(\Leftrightarrow-9x+63=0\)
\(\Leftrightarrow x=7\)

b: \(\Leftrightarrow\dfrac{7x+10}{x+1}\left(x^2-x-2-2x^2+3x+5\right)=0\)
\(\Leftrightarrow\left(7x+10\right)\left(-x^2+2x+3\right)=0\)
\(\Leftrightarrow\left(7x+10\right)\left(x^2-2x-3\right)=0\)
=>(7x+10)(x-3)=0
hay \(x\in\left\{-\dfrac{10}{7};3\right\}\)
d: \(\Leftrightarrow\dfrac{13}{2x^2+7x-6x-21}+\dfrac{1}{2x+7}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\dfrac{13}{\left(2x+7\right)\left(x-3\right)}+\dfrac{1}{\left(2x+7\right)}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)
\(\Leftrightarrow26x+91+x^2-9-12x-14=0\)
\(\Leftrightarrow x^2+14x+68=0\)
hay \(x\in\varnothing\)

a, \(6x^2-5x+3=2x-3x\left(3-2x\right)\)
⇔ \(6x^2-5x+3=2x-9x+6x^2\)
⇔ \(6x^2-5x+3-6x^2+9x-2x=0\)
⇔ \(2x+3=0\)
⇔ \(2x=-3\)
⇔ \(x=-\dfrac{3}{2}\)
b, \(\dfrac{2\left(x-4\right)}{4}-\dfrac{3+2x}{10}=x+\dfrac{1-x}{5}\)
⇔ \(\dfrac{20\left(x-4\right)}{4.10}-\dfrac{4\left(3+2x\right)}{4.10}=\dfrac{5x}{5}+\dfrac{1-x}{5}\)
⇔ \(\dfrac{20x-80}{40}-\dfrac{12+8x}{40}=\dfrac{5x+1-x}{5}\)
⇔ \(\dfrac{20x-80-12-8x}{40}=\dfrac{4x+1}{5}\)
⇔ \(\dfrac{12x-92}{40}-\dfrac{4x+1}{5}=0\)
⇔ \(\dfrac{12x-92}{40}-\dfrac{8\left(4x+1\right)}{40}=0\)
⇔ \(12x-92-8\left(4x+1\right)=0\)
⇔ 12x - 92 - 32x - 8 = 0
⇔ -100 - 20x = 0
⇔ 20x = -100
⇔ x = -100 : 20
⇔ x = -5

Bài 1:
a) \(\dfrac{3x^2-5}{x^2-5x}+\dfrac{5-15x}{5x-25}\)
\(=\dfrac{3x^2-5}{x\left(x-5\right)}+\dfrac{5\left(1-3x\right)}{5\left(x-5\right)}\)
\(=\dfrac{3x^2-5}{x\left(x-5\right)}+\dfrac{1-3x}{x-5}\)
\(=\dfrac{3x^2-5}{x\left(x-5\right)}+\dfrac{x\left(1-3x\right)}{x\left(x-5\right)}\)
\(=\dfrac{3x^2-5+x\left(1-3x\right)}{x\left(x-5\right)}\)
\(=\dfrac{3x^2-5+x-3x^2}{x\left(x-5\right)}\)
\(=\dfrac{-5+x}{x\left(x-5\right)}\)
\(=\dfrac{x-5}{x\left(x-5\right)}\)
\(=\dfrac{1}{x}\)
b) \(\dfrac{4+x^3}{x-3}-\dfrac{2x+2x^2}{x-3}+\dfrac{2x-13}{x-3}\)
\(=\dfrac{\left(4+x^3\right)-\left(2x+2x^2\right)+\left(2x-13\right)}{x-3}\)
\(=\dfrac{4+x^3-2x-2x^2+2x-13}{x-3}\)
\(=\dfrac{x^3-2x^2-9}{x-3}\)
\(=\dfrac{x^3-3x^2+x^2-9}{x-3}\)
\(=\dfrac{x^2\left(x-3\right)+\left(x-3\right)\left(x+3\right)}{x-3}\)
\(=\dfrac{\left(x-3\right)\left(x^2+x+3\right)}{x-3}\)
\(=x^2+x+3\)
c) \(\dfrac{2}{x-5}+\dfrac{x-25}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{2\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}+\dfrac{x-25}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{2\left(x+5\right)+x-25}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{2x+10+x-25}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{3x-15}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{3\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{3}{x+5}\)
d) Đề sai?
Bài 2:
\(A=2\left(x+1\right)+\left(3x+2\right)\left(3x-2\right)-9x^2\)
\(A=2x+2+9x^2-4-9x^2\)
\(A=2x-2\)
\(A=2\left(x-1\right)\)
Thay x = 15 vào A ta được:
\(A=2\left(15-1\right)\)
\(A=2.14=28\)

4)a)\(\dfrac{x+5}{x-5}-\dfrac{x-5}{x+5}=\dfrac{20}{x^2-25}\)(1)
ĐKXĐ:\(\left\{{}\begin{matrix}x-5\ne0\\x+5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne5\\x\ne-5\end{matrix}\right.\)
(1)\(\Rightarrow\left(x+5\right)\left(x+5\right)-\left(x-5\right)\left(x-5\right)=20\)
\(\Leftrightarrow x^2+10x+25-\left(x^2-10x+25\right)=20\)
\(\Leftrightarrow x^2+10x+25-x^2+10x-25=20\)
\(\Leftrightarrow x^2-x^2+10x+10x=-25+25=20\)
\(\Leftrightarrow20x=20\)
\(\Leftrightarrow x=1\left(nh\text{ậ}n\right)\)
S=\(\left\{1\right\}\)

Câu 2:
ĐKXĐ: \(\left[{}\begin{matrix}1-9x^2\ne0\\1+3x\ne0\\1-3x\ne0\end{matrix}\right.\Rightarrow \left[{}\begin{matrix}x\ne\dfrac{-1}{3}\\x\ne\dfrac{1}{3}\end{matrix}\right.\)
\(\dfrac{12}{1-9x^2}=\dfrac{1-3x}{1+3x}-\dfrac{1+3x}{1-3x}\left(1\right)\)
\(\left(1\right):\dfrac{12}{\left(1-3x\right)\left(1+3x\right)}-\dfrac{\left(1-3x\right)\left(1-3x\right)}{\left(1-3x\right)\left(1+3x\right)}+\dfrac{\left(1+3x\right)\left(1+3x\right)}{\left(1-3x\right)\left(1+3x\right)}=0\)
\(\Leftrightarrow 12-\left(1-3x-3x+9x^2\right)+\left(1+3x+3x+9x^2\right)=0\)
\(\Leftrightarrow 12-1+3x+3x-9x^2+1+3x+3x+9x^2=0\)
\(\Leftrightarrow12x+12=0\\ \Leftrightarrow12x=-12\\ \Leftrightarrow x=-1\left(TM\right)\)
Vậy \(S=\left\{-1\right\}\)
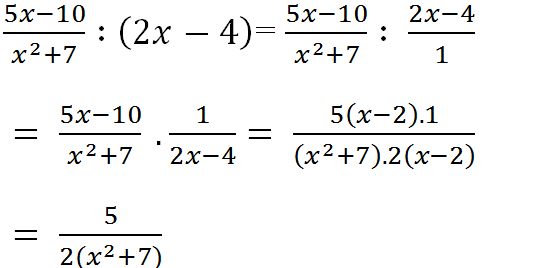


\(a,=\dfrac{\left(x-5\right)\left(x+5\right)\left(3x-7\right)}{2\left(x+5\right)}=\dfrac{\left(x-5\right)\left(3x-7\right)}{2}\\ b,=\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-1\right)}\cdot\dfrac{x-1}{x\left(x+2\right)}=\dfrac{x-2}{x^2}\)
a) \(\left(x^2-25\right):\dfrac{2x+10}{3x-7}=\left(x-5\right)\left(x+5\right).\dfrac{3x-7}{2\left(x+5\right)}=\dfrac{\left(x-5\right)\left(3x-7\right)}{2}\)
b) \(\dfrac{x^2-4}{x^2-x}:\dfrac{x^2+2x}{x-1}=\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}.\dfrac{x-1}{x\left(x+2\right)}=\dfrac{x-1}{x^2}\)