Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

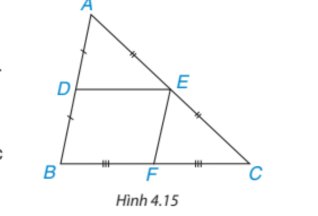
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

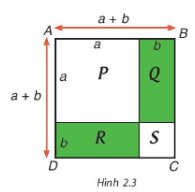
Diện tích hình vuông ABCD là: \({\left( {a + b} \right)^2}\)
Diện tích hình vuông ABCD là: \({S_{ABCD}} = {S_P} + {S_Q} + {S_R} + {S_S} = {a^2} + ab + ab + {b^2} = {a^2} + 2ab + {b^2}\)
Do đó \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)

Tham khảo:
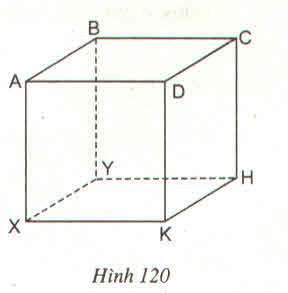
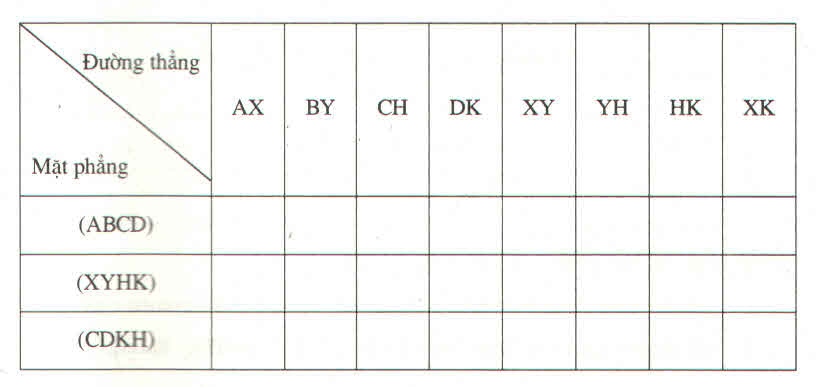
a. Những cặp mặt phẳng song song với nhau là:
mp (ABCD) và mp (XYHK)
mp (ADKX) và mp (BCHY)
mp (ABYX) và mp (CDKH)
b. Những cặp mặt phẳng vuông góc với nhau là:
mp (ABCD) và mp (ADKX); mp (XYHK) và mp (ADKX)
mp (ABCD) và mp (ABYX); mp (XYHK) và mp (ABYX)
mp (ABCD) và mp (BCHY); mp (XYHK) và mp (BCHY)
mp (ABCD) và mp (CDKH); mp (XYHK) và mp (CDKH)
mp (ADKX) và mp (CDKH); mp (ADKX) và mp (ABYX)
mp (BCHY) và mp (CDKH); mp (BCHY) và mp (ABYX)
c. Hai mặt phẳng (BCHY) và (KXYH) vuông góc với nhau.
d: 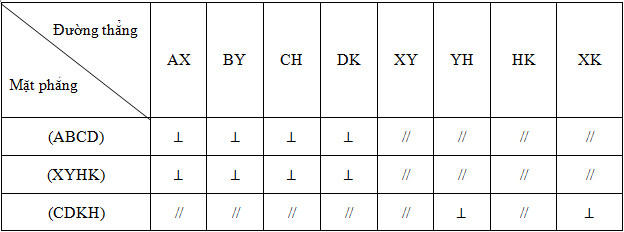

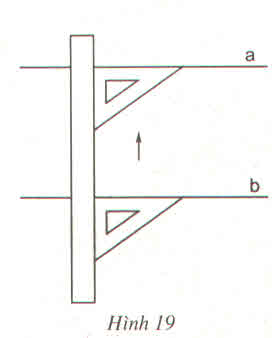
Các bước tiến hành:
- Xét xem cần phải kiểm tra hai cạnh nào thuộc hai đường thẳng song song với nhau.
- Đặt mép cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra.
- Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke.
- Giữ nguyên vị trí thước, dời êke để xét xem cạnh góc vuông của êke có trùng với cạnh còn lại mà ta cần kiểm tra của tứ giác. Nếu chúng trùng nhau thì tứ giác đó là hình thang.
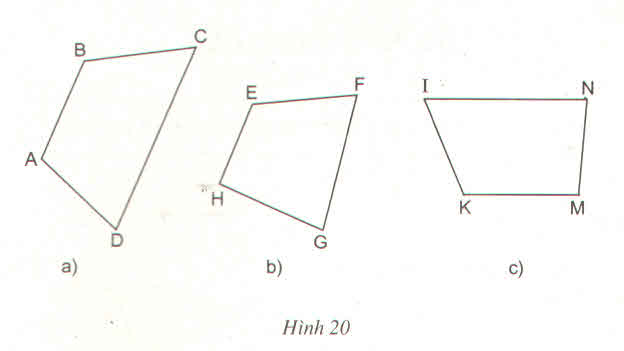
Các tứ giác ABCD, IKMN là hình thang.
Tứ giác EFGH không là hình thang.
Bài giải:
Các bước tiến hành:
- Xét xem cần phải kiểm tra hai cạnh nào thuộc hai đường thẳng song song với nhau.
- Đặt mép cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra.
- Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke.
- Giữ nguyên vị trí thước, dời êke để xét xem cạnh góc vuông của êke có trùng với cạnh còn lại mà ta cần kiểm tra của tứ giác. Nếu chúng trùng nhau thì tứ giác đó là hình thang.
Các tứ giác ABCD, IKMN là hình thang.
Tứ giác EFGH không là hình thang.

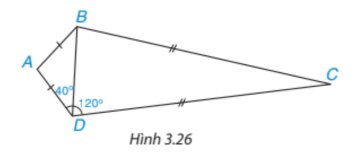
* Xét tam giác ABD cân tại A (vì AB = AD) ta có:
• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {40^o}\)
• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\)
Suy ra \(\widehat A\)=180°−\(\widehat {AB{\rm{D}}}\)−\(\widehat {A{\rm{D}}B}\)=180°−40°−40°=100°
Ta có \(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C}\)=120° suy ra \(\widehat {B{\rm{D}}C}\)=120°−\(\widehat {A{\rm{D}}B}\)=120°−40°=80°.
* Xét tam giác BCD cân tại C (vì BC = CD) ta có:
• \(\widehat {CB{\rm{D}}} = \widehat {C{\rm{D}}B}\)=80°
• \(\widehat C + \widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B}\)=180°
Suy ra \(\widehat C\)=180°−\(\widehat {CB{\rm{D}}} - \widehat {C{\rm{D}}B}\)=180°−80°−80°=20°
Ta có: \(\widehat {ABC} = \widehat {AB{\rm{D}}} + \widehat {CB{\rm{D}}}\)=40°+80°=120o
Vậy số đo các góc của tứ giác ABCD là \(\widehat A = {100^o};\widehat {ABC} = {120^o};\widehat C = {20^o}\)

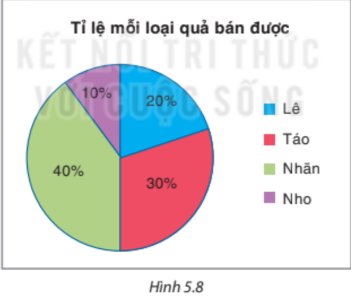
Theo đề bài, cửa hàng bán được 200 kg quả các loại. Khi đó:
• Số quả lê cửa hàng đó bán được là: 200 . 20% = 40 (quả);
• Số quả táo cửa hàng đó bán được là: 200 . 30% = 60 (quả);
• Số quả nhãn cửa hàng đó bán được là: 200 . 40% = 80 (quả);
• Số quả nho cửa hàng đó bán được là: 200 . 10% = 20 (quả);
Bảng thống kê số lượng mỗi loại quả cửa hàng bán được:
Loại quả | Lê | Táo | Nhãn | Nho |
Số lượng (quả) | 40 | 60 | 80 | 20 |
Biểu đồ cột số lượng mỗi loại quả cửa hàng bán được:


a: Ta có thể làm được điều đó. Bởi tứ giác chỉ cần 3 góc vuông đã là hình chữ nhật rồi
b: Khung cửa sổ là hình chữ nhật