Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

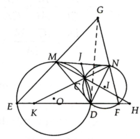
a, Ta có: D M N ^ = E ^ = G M N ^ , D N M ^ = N F D ^ = G N M ^
=> ∆GMN = ∆DMN
b, Chứng minh được MN là đường trung trực của GD
=> GD ⊥ EF (1)
Gọi J là giao điểm của DC và MN
Ta có J M D H = J N D K C J C D
Mặt khác: JM = JN (cùng bằng J C . J D )
=> DH = DK (2). Từ (1) và (2) Þ ĐPCM

a) góc HEC = góc CAM = góc CBH.
b) CM EB2 = EC.EA = EM2 từ đó ta có góc EMC = góc EAM = góc ADC suy ra AD song song MB. Do đó góc BDA = góc ABM = góc BAD.
c) Ta có BJ là đường kính và BJ vuông góc với AD tại K (AD song song MB). Do đó KD = KA
Bằng miệng
CÂM MỒM