
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Xét tam giác ABH và tam giác ADH có:
HB=HD (gt)
\(\widehat{BHA}=\widehat{DHA}\left(=90\right)\)
HA chung
=> Tam giác ABH=tam giác ADH (c-g-c)
=> AB=AD
=> tam giác ABD cân tại A
b) Ta có: tam giác ABH=tam giác ADH (câu a)
=> \(\widehat{HAB}=\widehat{HAD}\) (2 góc tương ứng) (1)
Ta lại có: \(\widehat{HAB}=\widehat{BAC}-\widehat{HAC}\) = \(90-\widehat{HAC}\)
\(\widehat{ACH}=\widehat{CHA}-\widehat{HAC}=90-\widehat{HAC}\)
=> \(\widehat{HAB}=\widehat{ACH}\) (2)
Từ (1) và (2) => \(\widehat{HAD}=\widehat{ACH}\) (*) (đpcm)
Xét tam giác AEM và tam giác CHM có:
\(\widehat{M}\) chung
\(\widehat{AEM}=\widehat{CHM}=90\)
=> tam giác AEM = tam giác CHM
=> \(\widehat{HAD}=\widehat{MCH}\) ( 2 góc tương ứng) (**)
Từ (*) và (**) => \(\widehat{ACH}=\widehat{MCH}\)
=> CB là tia phân giác của \(\widehat{ACM}\) (đpcm)
Còn câu d mình chưa biết
Nếu mà sai thì bạn thông cảm nha ![]()

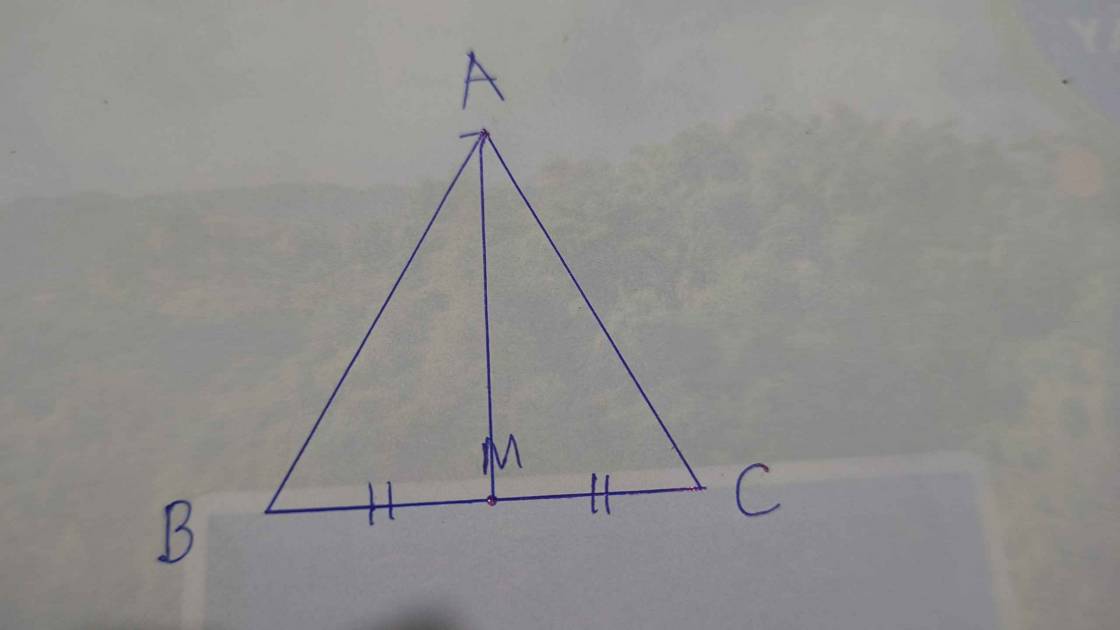
a) Xét △ ABM và △ECM có:
BM=MC (vì M là trung điểm của BC)
AM=ME (giả thiết cho)
\(\widehat{AMB}=\widehat{EMC}\) (đối đỉnh)
Vậy ΔABM=ΔECM(c.g.c)
b) Vì ΔABM=ΔECM (chứng minh trên) nên\(\widehat{BAM}=\widehat{E}\) (2 góc tương ứng)
Mà đây là 2 góc so le trong nên suy ra AB // CE
c) Vì ΔAMB=ΔECM (chứng minh trên) nên AB=CE (2 cạnh tương ứng)

a: Xét ΔMAC và ΔMDB có
MA=MD
góc AMC=góc DMB
MC=MB
=>ΔMAC=ΔMDB
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC//BD
c: Xét tứ giác BFCE có
BF//CE
BF=CE
=>BFCE là hình bình hành
=>BC cắt FE tại trung điểm của mỗi đường
=>M,E,F thẳng hàng

Bạn tham khảo tại đây nhé: Câu hỏi của Trúc Huỳnh.
Chúc bạn học tốt!

a) ta có: AD =AB (gt)
⇒AC là trung tuyến ΔBDC
mà AE =1/3AC(gt)
⇒E là trọng tâm Δ BDC
mà BM qua E
⇒BM là trung tuyến ΔBDC
⇒M là trung điểm CD

a: Xét ΔAEM vuông tại E và ΔAFC vuông tại F có
AM=AC
\(\widehat{EAM}=\widehat{FAC}\)
Do đo: ΔAEM=ΔAFC
Suy ra: AE=AF
hay A là trung điểm của FE
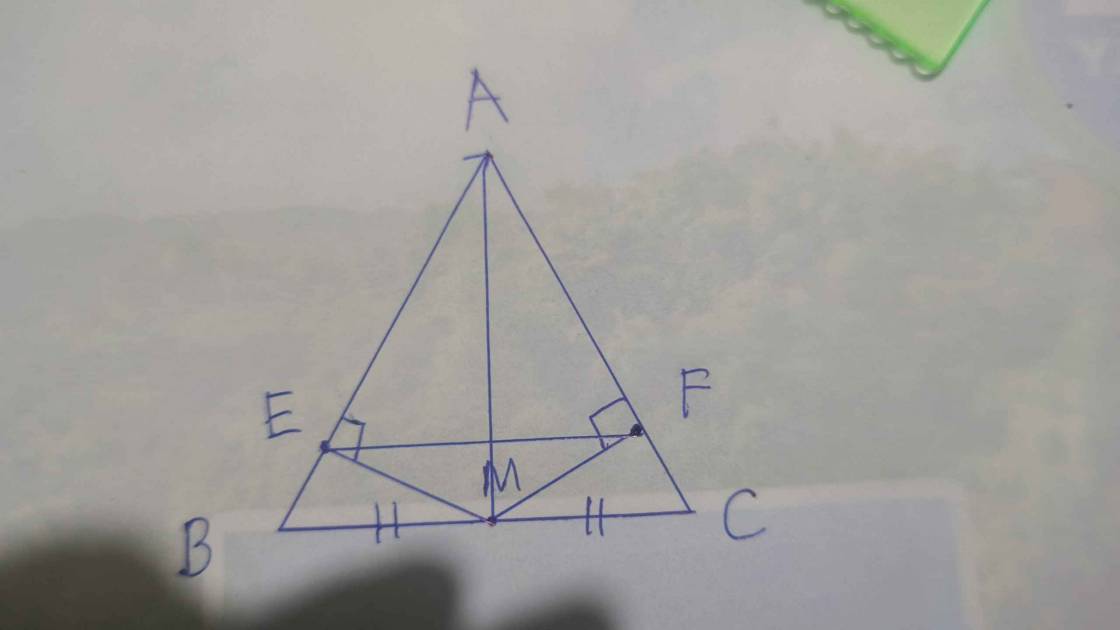
b: Xét tứ giác MFCE có
A là trung điểm của FE
A là trung điểm của MC
Do đó: MFCE là hình bình hành
Suy ra: MF//CE

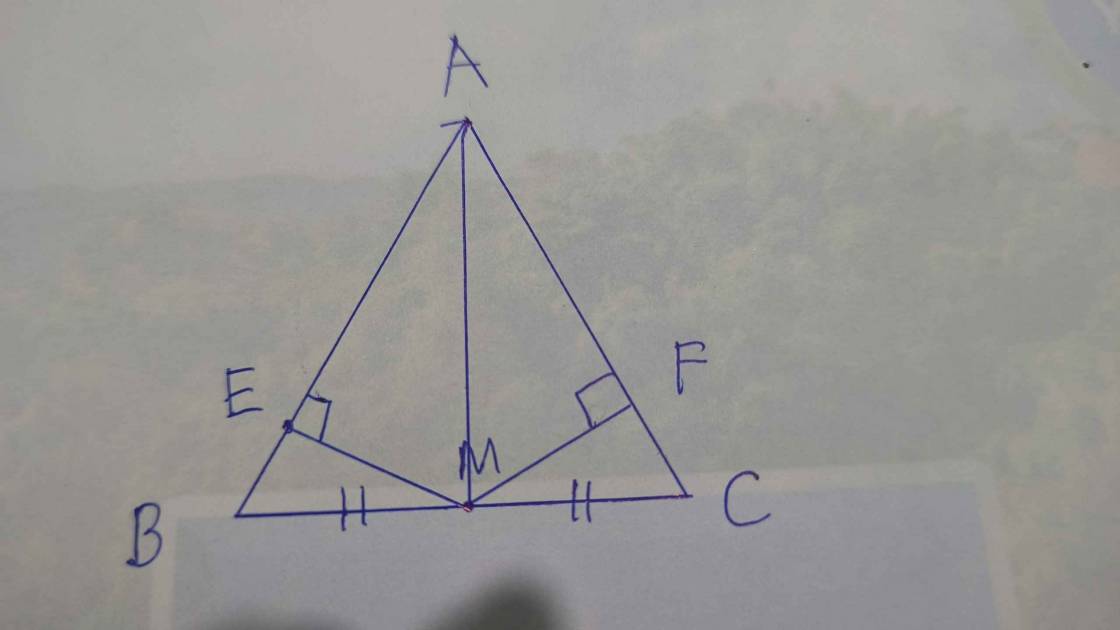
https://olm.vn/thanhvien/songoku1a90 Đề sai !