a) Chứng minh nếu x + y + z = 0 thì = 3xyz.
b) Áp dụng. Phân tích các đa thức sau thành nhân tử:
P = .

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Chứng minh nếu x + y + z = 0 thì = 3xyz.
b) Áp dụng. Phân tích các đa thức sau thành nhân tử:
P = .

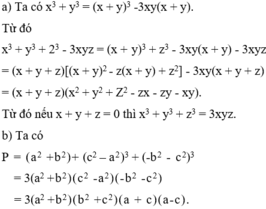

a) \(x^3+y^3+z^3-3xyz\)
\(=x^3+3x^2y+3xy^2+y^3+z^3-3x^2y-3xy^3-3xyz\)
\(=\left(x+y\right)^3+z^3-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-\left(x+y\right)z+z^2\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2\right)-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)

Ta có : \(x+y+z=0\)
\(\Leftrightarrow x+y=-z\) \(\Leftrightarrow\left(x+y\right)^3=-z^3\)
\(\Leftrightarrow x^3+3x^2y+3xy^2+y^3=-z^3\)
\(\Leftrightarrow x^3+y^3+z^3=-3xy\left(x+y\right)\)
\(\Leftrightarrow x^3+y^3+z^3=3xyz\)
* Áp dụng :
Ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\Leftrightarrow ab+bc+ca=0\)
\(\Leftrightarrow a^3b^3+b^3c^3+c^3a^3=3ab.bc.ca=3a^2b^2c^2\)
Khi đó \(M=\frac{ab}{c^2}+\frac{bc}{a^2}+\frac{ca}{b^2}=\frac{a^3b^3+b^3c^3+c^3a^3}{a^2b^2c^2}=\frac{3a^2b^2c^2}{a^2b^2c^2}=3\)

a, x^3 + y^3 + z^3 = (x+y)^3 - 3xy(x+y) + z^3
= (x+y+z)[(x+y)^2 - (x+y)z + z^2] - 3xy(x+y)
= -3xy(x+y) (do x+y+z=0)
Vì x+y+z=0 =>x+y=-z
=> -3xy(x+y)=3xyz
Bài này có nhiều cách giải bạn cũng có thể dựa vào x+y+z=0 => x=-(y+z),....... rồi thay vào
Và sau này khi giải các bài toán thì bạn có thể AD: Nếu x+y+z=0 thì x^3 +y^3+z^3=3xyz

x(y+z)^2 - y(z-x)^2 +z(x+y)^2 - x^3 + y^3 - z^3 - 4xyz
=xy^2+2xyz+xz^2-yz^2+2xyz-x^2y+x^2z+2xyz+zy^2-x^3+y^3-z^3-4xyz
=xy^2+xz^2-yz^2-x^2y+x^2z+y^2z-x^3+y^3-z^3+2xyz
=(xy^2+2xyz+xz^2)-x^3-(yz^2+2xyz+x^2y)+y^3+(x^2z+2xyz+y^2z)-z^3
=x[(y+z)^2-x^2)-y[(z+x)^2-y^2]+z[(x+y)^2-z^2]
=x(-x+y+z)(x+y+z)-y(x-y+z)(x+y+z)+z(x+y-z)(x+y+z)
=(x+y+z)[-x^2+xy+xz-xy+y^2-yz+xz+yz-z^2]
=(x+y+z)[-x(x-y-z)-y(x-y-z)+z(x-y-z)]
=(x+y+z)(x-y-z)(z-x-y)

Câu a bạn xét giá trị riêng nha
A=x2(y-z) + y2(z-x) + z2(x-y)
Thay x bởi y, ta có
A= y2 (y-z) + y2(z-y) + z2(y-y) = 0
=> A chứa nhân tử x-y
Tương tự A chứa nhân tử y-z, z-x
=> A có tích (x-y)(y-z)(z-x)
Ta thấy biểu thức A có bậc 3, tích (x-y)(y-z)(z-x) cũng có bậc là 3 nên A có dạng tổng quát: A= k(x-y)(y-z)(z-x) ( k thuộc R)
Ta có đẳng thức : x2(x-y) + y2(z-x) +z2( x-y) = k(x-y)(y-z)(z-x) với mọi x,y,z
Cho x=0,y=1,z=2 => -2 = 2k => k=-1
Vậy A= -(x-y)(y-z)(z-x)
b) a7 + a +1 = a7 + a6 - a6 - a5 +a5 + a4 -a4 - a3 + a3 + a2 +a +1
= a6 (a+1) - a5 (a+1) +a4 (a+1) -a3 (a+1) +a2(a+1) +(a+1)
=(a+1)( a6 - a5 + a4 - a3 + a2 +1)

đừng tin Tên đẹp thật
cậu ta lừa bn lik e rùi ko giải đâu