Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Gọi I là Trung điểm CD => IC = ID
Xét hình thang AEFB , I là trung điểm EF => IE=IF
Từ đó suy ra CE=DF
b, Ta có E A B ^ và F B A ^ bù nhau nên có một góc tù và một góc nhọn
Giả sử E A B ^ > 90 0 => ∆EAO có OE > AO = R => E ở ngoài đường tròn mà OE = OF nên F cũng ở ngoài đường tròn

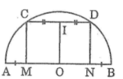
Ta có: MC // ND (gt)
Suy ra tứ giác MCDN là hình thang
Lại có: OM + AM = ON + BN (= R)
Mà AM = BN (gt)
Suy ra: OM = ON
Kẻ OI ⊥ CD (3)
Suy ra: IC = ID (đường kính dây cung)
Khi đó OI là đường trung bình của hình thang ACDN
Suy ra: OI // MC // ND (4)
Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.

a: Xét (O) có
OM là bán kính
EF vuông góc OM tại M
Do đó: EF là tiếp tuyến của (O)
b: Xét (O) có
EM.EA là tiếp tuyến
nên EM=EA
Xét(O) có
FM,FB là tiếp tuyến
nên FM=FB
EF=EM+MF
=>EF=EA+FB

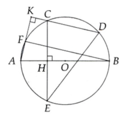
a, HS tự chứng minh
b, Từ giả thiết ta có AB là đường trung trực của CE => B C ⏜ = B E ⏜ = B F ⏜ = D E ⏜
c, Sử dụng mối liên hệ cung và dây
