Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

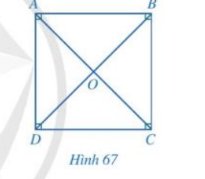
a, Hình chữ nhật ABCD có AB = BC
Suy ra hình chữ nhật ABCD có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^0};AB = BC = CD = DA\)
Suy ra hình chữ nhật ABCD là hình vuông
b, O là giao điểm của AC và BD.
Vì ABCD là hình chữ nhật nên OB = OD.
Mà AC vuông góc BD. Suy ra AC là đường trung trực của đoạn thẳng BD.
Xét \(\Delta ABD\) có AO vừa là đường trung trực vừa là đường cao
\( \Rightarrow \Delta ABD \) là tam giác vuông cân tại A.
\( \Rightarrow AB = AD\)
Mà AB = CD, AD = BC (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.
c, Ta có ABCD là hình chữ nhật nên \(\widehat A =\widehat B = \widehat C = \widehat D = 90^0\)
Vì AC là tia phân giác của góc DAB nên ta có: \(\widehat{DAC} = \widehat{CAB} =\frac{\widehat{DAB}}{2} = \frac{90^0}{2} = 45^0\)
Xét tam giác ABC vuông tại B (\(\widehat B = 90^0\)), ta có:
\(\widehat{ACB} + \widehat B + \widehat{CAB} = 180^0\)
\(\Rightarrow \widehat{ACB} = 180^0 - \widehat B - \widehat{CAB} = 180^0 - 90^0 - 45^0 = 45^0\)
\( \Rightarrow \widehat{ACB} = \widehat{CAB} =45^0\) nên tam giác ABC vuông cân tại B.
\( \Rightarrow AB = BC\)
Mà AB = CD, BC = AD (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

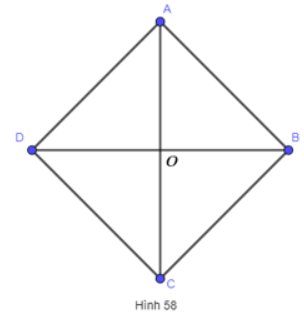
a) Hình thoi ABCD có là hình bình hành (vì AB = BC = CD = DA)
b) Xét tam giác ABD có AB = AD nên tam giác ABD là tam giác cân tại A.
Suy ra đường trung tuyến AO đồng thời là đường cao.
Suy ra AO vuông góc với BD
Hay AC vuông góc với BD
c) Xét tam giác ABC và tam giác ADC có:
AD = AB
CD = CB
AC chung
\(\begin{array}{l}\Delta ABC = \Delta A{\rm{D}}C\\ \Rightarrow \widehat {DAC} = \widehat {BAC}\end{array}\)
Mà AC nằm giữa 2 tia AB và AD
Suy ra: AC là tia phân giác của góc BAD

Bai 1:
Ta co: BD la duong cheo vua la duong phan giac ( T/c cua duong cheo trong hinh thoi )
Thay co goc B = 120 cm, suy ra goc ABC = 60 do
Tam giac ABC la tam giac deu
AB = AD = BD = 5

Theo chứng minh ở câu a. △ AEB đồng dạng △ ABC theo tỉ số k = 1/2 nên dễ thấy BE = 1/2 BC hay BE = BM
Suy ra: ΔBEM cân tại B.
Xét tam giác EBC có: 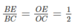
Suy ra: OB là đường phân giác góc EBC
BO là đường phân giác góc ở đỉnh của tam giác cân BEM nên BO vuông góc với cạnh đáy EM (đpcm).
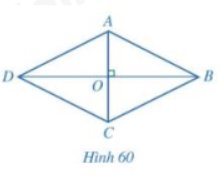


a) Hình bình hành ABCD có AB = BC
Suy ra: AB = BC = CD = DA
Nên hình bình hành ABCD là hình thoi
b) AC giao điểm với BD tại O
Ta có: O là trung điểm của BD (do ABCD là hình bình hành)
AO vuông góc với BD
Suy ra AO là đường trung trực của đoạn thẳng BD
Suy ra tam giác ABD cân tại A
Suy ra: AB = AD
Suy ra AB = DC = AD = BC
Hình bình hành ABCD là hình thoi