Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Có \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOA'B' ∽ ΔOAB (c.g.c)
- Có \(\frac{{OC'}}{{OC}} = \frac{{OB'}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOB'C' ∽ ΔOBC(c.g.c)
=> ΔABC ∽ ΔA'B'C' (c.g.c)
- Đường thẳng có đi qua O

Tự vẽ hình.
a) Xét tam giác OAB có AB // CD
⇒AOOC=OBOD=ABDC⇒12OC=93=18DC⇒AOOC=OBOD=ABDC⇒12OC=93=18DC ( Hệ quả định lý Ta - lét ) (1)
=> OC = 4cm, DC = 6cm
Vậy OC = 4cm và DC = 6cm
b) Xét tam giác FAB có DC // AB
⇒FDAD=FCCB⇒FD.BC=FC.AD⇒FDAD=FCCB⇒FD.BC=FC.AD ( ĐPCM )
c) Theo (1), ta đã có:
OAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBDOAOC=OBOD⇒OAOA+OC=OBOB+OD⇒OAAC=OBBD (2)
Vì MN // AB mà AB // DC => MN // DC
Xét tam giác ADC có MO// DC
⇒MODC=AOAC⇒MODC=AOAC ( Hệ quả định lý Ta - lét ) (3)
CMTT : ONDC=OBDBONDC=OBDB (4)
Từ (2), (3) và (4) => MODC=NODC⇒MO=NOMODC=NODC⇒MO=NO ( ĐPCM )

Xét ΔOAB có
M∈OA(gt)
N∈OB(gt)
\(\dfrac{OM}{OA}=\dfrac{ON}{OB}\left(=\dfrac{1}{3}\right)\)
Do đó: MN//AB(Định lí Ta lét đảo)
Xét ΔOAB có
M∈OA(gt)
N∈OB(gt)
MN//AB(cmt)
Do đó: \(\dfrac{MN}{AB}=\dfrac{OM}{OA}\)(Hệ quả của Định lí Ta lét)
⇔\(\dfrac{MN}{AB}=\dfrac{1}{3}\)(1)
Xét ΔAOC có
M∈OA(gt)
P∈OC(gt)
\(\dfrac{OM}{OA}=\dfrac{OP}{OC}\left(=\dfrac{1}{3}\right)\)
Do đó: MP//AC(Định lí Ta lét đảo)
Xét ΔOAC có
M∈OA(gt)
P∈OC(gt)
MP//AC(cmt)
Do đó: \(\dfrac{MP}{AC}=\dfrac{OM}{OA}\)(Hệ quả của Định lí ta lét)
hay \(\dfrac{MP}{AC}=\dfrac{1}{3}\)(2)
Xét ΔOBC có
N∈BO(gt)
P∈CO(gt)
\(\dfrac{ON}{OB}=\dfrac{OP}{OC}\left(=\dfrac{1}{3}\right)\)
Do đó: NP//BC(Định lí Ta lét đảo)
Xét ΔOBC có
N∈BO(gt)
P∈CO(gt)
NP//BC(cmt)
Do đó: \(\dfrac{NP}{BC}=\dfrac{ON}{OB}\)(Hệ quả của Định lí Ta lét)
⇔\(\dfrac{NP}{BC}=\dfrac{1}{3}\)(3)
Từ (1), (2) và (3) suy ra \(\dfrac{MN}{AC}=\dfrac{MP}{AC}=\dfrac{NP}{BC}\)
Xét ΔMNP và ΔABC có
\(\dfrac{MN}{AC}=\dfrac{MP}{AC}=\dfrac{NP}{BC}\)(cmt)
Do đó: ΔMNP∼ΔABC(C-c-c)

A B C H A' O C' B'
kẻ đường cao AH có: \(\frac{OA'}{AA'}=\frac{S_{BOC}}{S_{ABC}}\), ta có:
\(\frac{OB'}{BB'}=\frac{S_{AOC}}{S_{ABC}}\)
\(\frac{OC'}{CC'}=\frac{S_{AOB}}{S_{ABC}}\)
\(\Rightarrow\frac{OA'}{AA'}+\frac{OB'}{BB'}+\frac{OC'}{CC'}=\frac{S_{BOC}+S_{AOC}+S_{AOB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\) (đpcm)
Nguồn: HiệU NguyễN


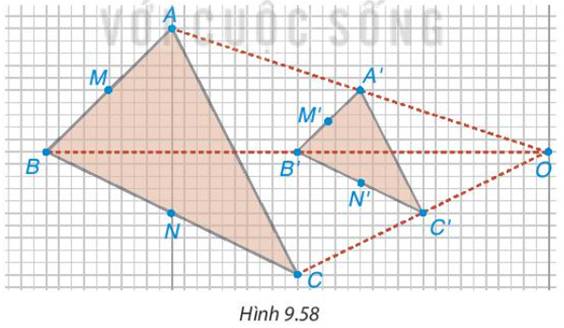
a)
i) Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\).
Xét tam giác \(OA'B'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{1}{3}\)
Do đó, \(A'B'//AB\) (định lí Thales đảo)
ii) Vì \(A'B'//AB \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'B'}}{{AB}} = \frac{3}{1} = 3\).
b)
i)
- Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\).
Xét tam giác \(OA'B'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{1}{3}\)
Do đó, \(A'B'//AB\) (định lí Thales đảo)
Vì \(A'B'//AB \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'B'}}{{AB}} = \frac{3}{1} = 3\).
- Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OC' = 3OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{3}\).
Xét tam giác \(OA'C'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OC}}{{OC'}} = \frac{1}{3}\)
Do đó, \(A'C'//AC\) (định lí Thales đảo)
Vì \(A'C'//AC \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OC}}{{OC'}} = \frac{{AC}}{{A'C'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'C'}}{{AC}} = \frac{3}{1} = 3\).
- Vì \(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\);\(OC' = 3OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{3}\).
Xét tam giác \(OB'C'\) có:
\(\frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{1}{3}\)
Do đó, \(B'C'//BC\) (định lí Thales đảo)
Vì \(B'C'//BC \Rightarrow \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{BC}}{{B'C'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{3}{1} = 3\).
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
ii) Xét tam giác \(A'B'C'\) và tam giác \(ABC\) ta có:
\(\frac{{B'C'}}{{BC}} = \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) (chứng minh trên)
Do đó, tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\).