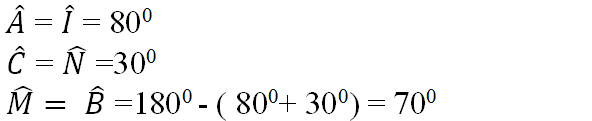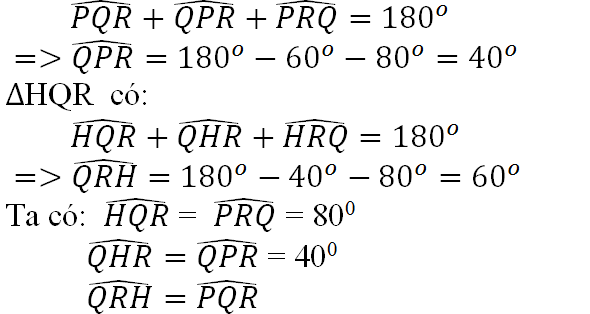Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

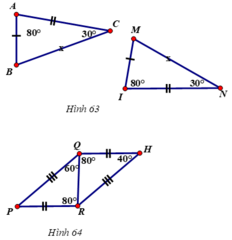
- Xem hình 63)
Ta có:
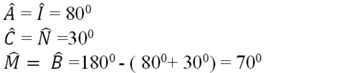
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
QUẢNG CÁO- Xem hình 64)
ΔPQR có:
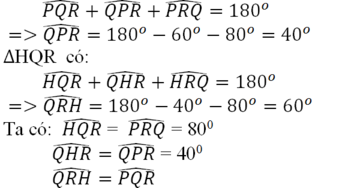
Và QH = RP, HR = PQ, QR cạnh chung
Nên ΔHQR = ΔPRQ

Xem hình a) ta có:
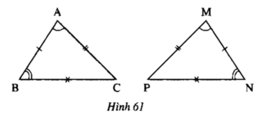
\(\widehat{A}=\widehat{I}=80^0\) ; \(\widehat{C}=\widehat{N}=30^0\)
\(\widehat{B}=\widehat{M}=180^0-\left(80^0+30^0\right)=70^0\)
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
\(\widehat{Q}_2=\widehat{R}_2=80^0\)=800 (ở vị trí so le trong)
Nên QH// RP
Nên \(\widehat{R}_1=\widehat{Q}_1\)= 600(so le trong)
\(\widehat{P}=\widehat{H}\)= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.
Xem hình a) ta có:
ˆAA^=ˆII^=800,ˆCC^=ˆNN^=300
ˆBB^=ˆMM^=1800-(800+300)=700
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
ˆQ2Q2^=ˆR2R2^=800 (ở vị trí so le trong)
Nên QH// RP
Nên ˆR1R1^ = ˆQ1Q1^= 600(so le trong)
ˆPP^=ˆHH^= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.

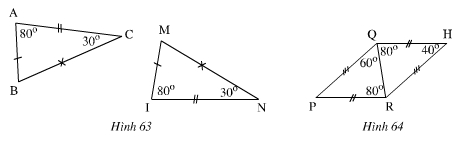
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ

Hai tam giác bằng nhau vì có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau
kí hiệu: ΔABC = ΔMNP

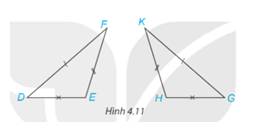
Các cặp cạnh tương ứng : FE = KH , ED = HG , DF = GK
Các góc tương ứng : góc F = góc K, góc E = góc H, góc D = góc G
Kí hiệu bằng nhau của tam giác đó : ΔDFE=ΔGKH
Ta có: Các cặp góc tương ứng là: \(\widehat E = \widehat H;\widehat D = \widehat G;\widehat F = \widehat K\)
Các cặp cạnh tương ứng là:\(ED=HG;EF=HK;DF=GK\)

tam giác ABC và tam giác HIK . vì AB = KI , góc B = góc K .
suy ra : AC=IH ; BC = KH