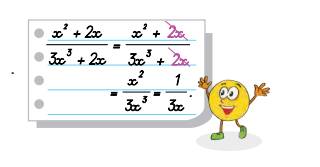Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

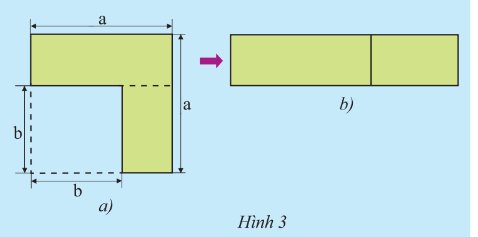
a) Diện tích Hình 3a là: \({a^2} - {b^2}\)
Diện tích Hình 3b là: \(\left( {a + b} \right)\left( {a - b} \right)\)
b) Ta có: \(\left( {a + b} \right)\left( {a - b} \right) = a.a - ab + ba - {b^2} = {a^2} - ab + ab - {b^2} = {a^2} - {b^2}\)
Suy ra: \(\left( {a + b} \right)\left( {a - b} \right) = {a^2} - {b^2}\)
Vậy diện tích của hai hình bằng nhau.

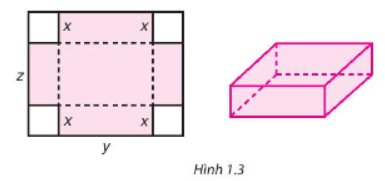
Hình gấp được là hình hộp chữ nhật có:
Chiều rộng là \(z - 2x\) (centimet)
Chiều dài là \(y - 2x\) (centimet)
Chiều cao là \(x\) (centimet)
Thể tích chiếc hộp là: \(\left( {z - 2x} \right).\left( {y - 2x} \right).x = \left( {zy - 2xz - 2xy + 4{x^2}} \right).x = xyz - 2{x^2}z - 2{x^2}y + 4{x^3}\) ( centimet khối)
Đa thức này có bậc là 3.

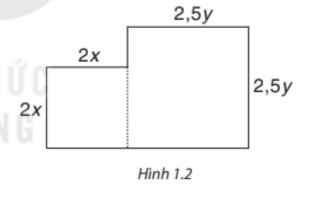
Diện tích hai hình vuông là: \(2x.2x + 2,5y.2,5y = 4{x^2} + 6.25{y^2}\)
Diện tích hai hình tròn là: \({\pi .{x^2} + \pi .{y^2}}\)
Diện tích phần còn lại của miếng bìa là:
\(\begin{array}{l}S = 4{x^2} + 6.25{y^2} - \pi .{x^2} - \pi .{y^2}\\ = \left( {4 - \pi } \right){x^2} + \left( {6,25 - \pi } \right){y^2}\end{array}\)
Biểu thức này là một đa thức, có bậc là 2.

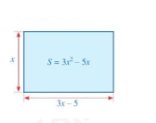
\(3{{\rm{x}}^2} - 5{\rm{x = x}}\left( {3{\rm{x}} - 5} \right)\)

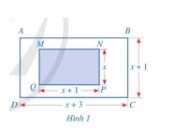
Biểu thức diện tích của hình chữ nhật ABCD là: \({S_{ABC{\rm{D}}}} = \left( {x + 1} \right)\left( {x + 3} \right)\)
Biểu thức diện tích của hình chữ nhật MNPQ là: \({S_{MNPQ}} = x\left( {x + 1} \right)\)
Tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNPQ là: \(\dfrac{{{S_{ABC{\rm{D}}}}}}{{{S_{MNPQ}}}} = \dfrac{{\left( {x + 1} \right)\left( {x + 3} \right)}}{{x\left( {x + 1} \right)}} = \dfrac{{x + 3}}{x}\)
b) Với x = 5 ta có: \(\dfrac{{{S_{ABC{\rm{D}}}}}}{{{S_{MNPQ}}}} = \dfrac{{5 + 3}}{5} = \dfrac{8}{5}\)
Với x = 2 ta có: \(\dfrac{{{S_{ABC{\rm{D}}}}}}{{{S_{MNPQ}}}} = \dfrac{{2 + 3}}{2} = \dfrac{5}{2}\)

a) Dựa vào biểu đồ Hình 5.17, ta có:
- Số tiền bán phế liệu của Tuyết là 280 nghìn đồng;
- Số tiền bán phế liệu của Khánh là 240 nghìn đồng.
Số tiền của Tuyết gấp số lần số tiền của Khánh là:\(\frac{{280}}{{240}} = \frac{7}{6} \approx 1,2\) (lần).
Trên biểu đồ Hình 5,17, xét về chiều cao của cột trên biểu đồ thì cột biểu diễn số tiền của Tuyết gấp đôi Khánh (số tiền của Tuyết chiếm 4 ô, còn số tiền của Khánh chiếm 2 ô). Tuy nhiên, trên biểu đồ chỉ biểu diễn giá trị từ 200 đến 360 (khoảng từ 0 đến 200 đã bị rút ngắn).
Do đó, số tiền của Tuyết không phải gấp đôi số tiền của Khánh.
b) Ta lập bảng thống kê cho số tiền mỗi bạn có được nhờ bán phế liệu như sau:
Tên các bạn trong nhóm | An | Bình | Tuyết | Khánh | Hải |
Số tiền (nghìn đồng) | 230 | 250 | 280 | 240 | 350 |

\(C=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\)
\(C=x^{64}-1-x^{64}\)
\(C=-1\)
Vậy gtri của C không phụ thuộc vào x

Bạn tròn làm thế là sai. Vì bạn bỏ hai số hạng giống nhau của cả tử và mẫu là 2x chứ không phải chia cho nhân tử chung của cả tử và mẫu.

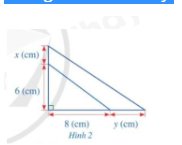
Diện tích hình tam giác vuông ban đầu là: \(\dfrac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Độ dài các cạnh của hình vuông sau khi tăng độ dài là: x + 6 (cm); y + 8 (cm)
Diện tích tam giác vuông sau khi tăng độ dài là: \(\dfrac{1}{2}\left( {x + 6} \right).\left( {y + 8} \right) = \dfrac{{{xy}}}{2} + 4x + 3y + 24\left( {c{m^2}} \right)\)
Đa thức biểu thị phần diện tích tăng thêm của miếng bìa là: \(\dfrac{{{xy}}}{2} + 4x + 3y + 24 - 24 = \dfrac{{{xy}}}{2} + 4x + 3y\left( {c{m^2}} \right)\)
Vậy đa thức biểu thị phần diện tích tăng thêm của miếng bìa là: \(\dfrac{{{xy}}}{2} + 4x + 3y\left( {c{m^2}} \right)\)