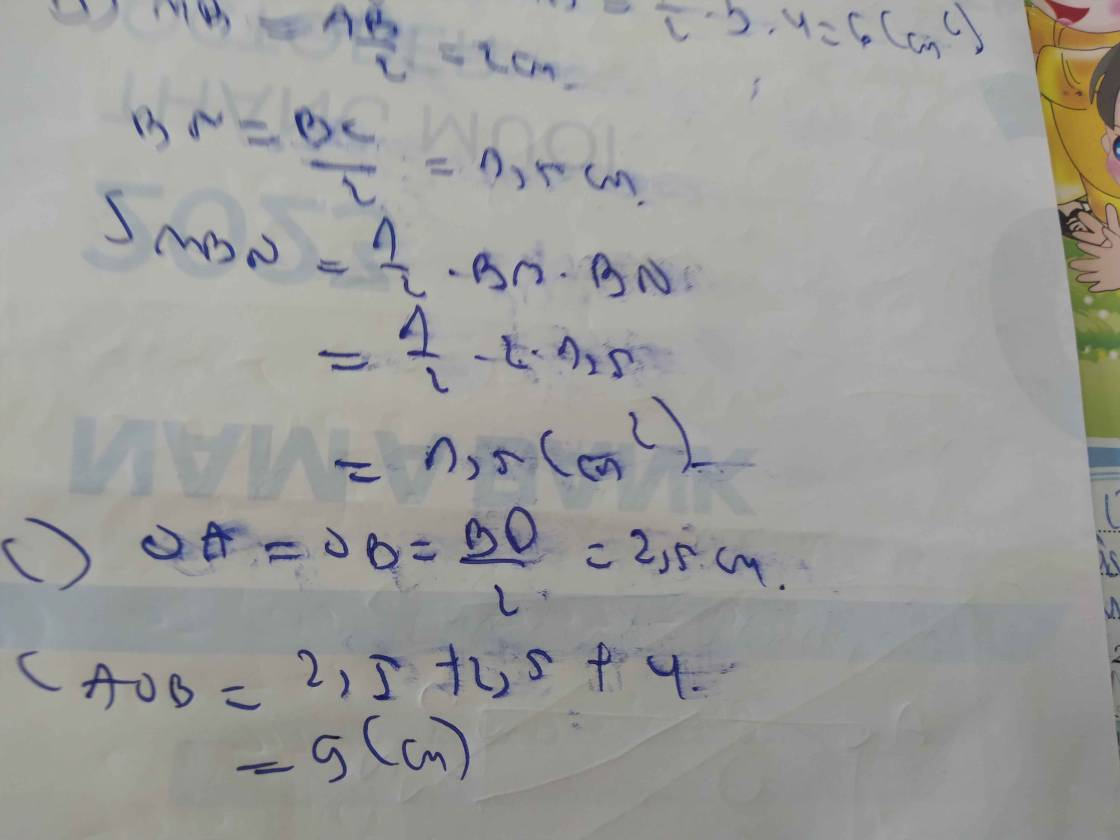K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 8 2018
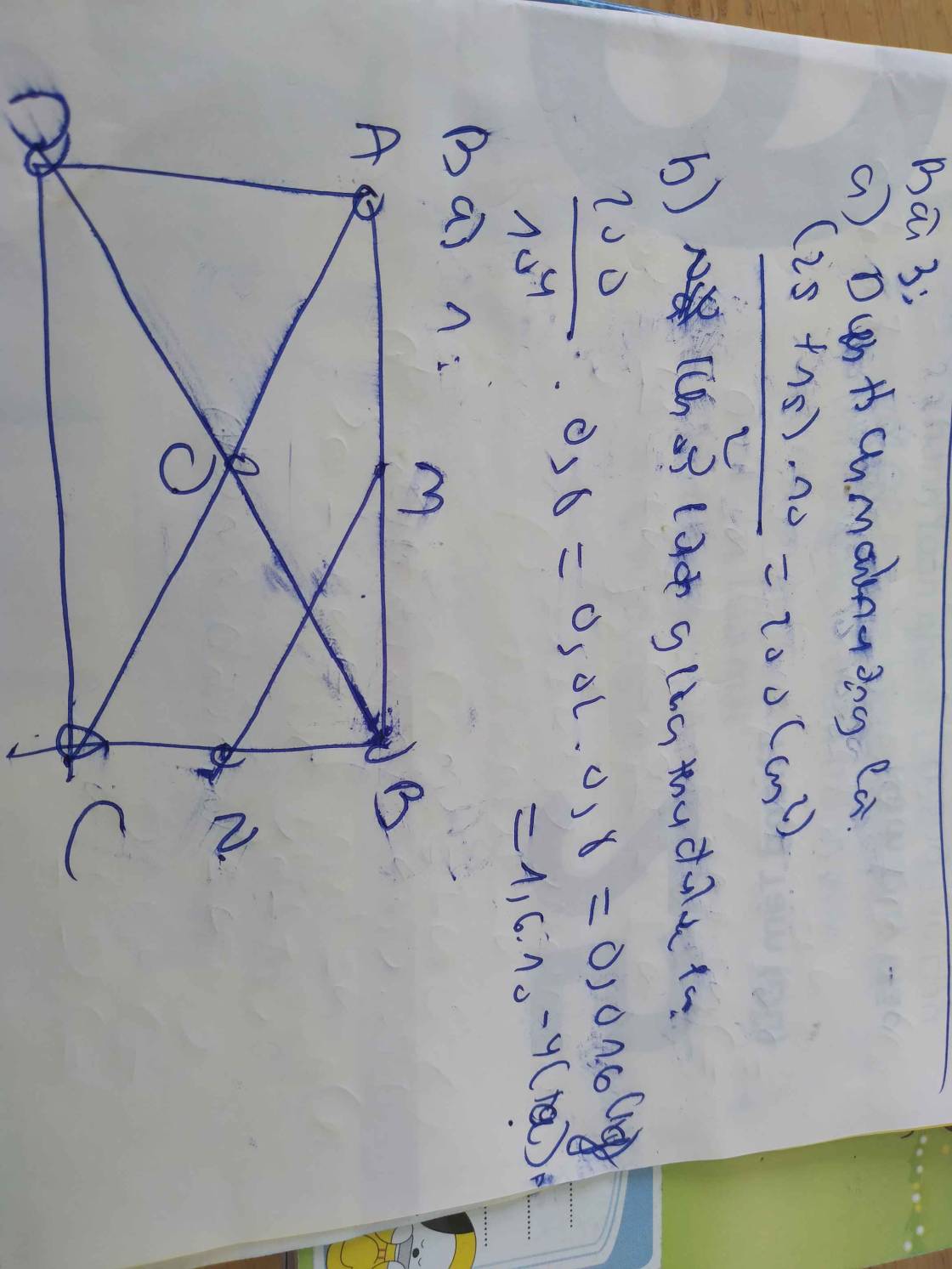
a, Xét \(\Delta ACM\)và \(\Delta BCD\)có :
MC = DC ( gt )
\(\widehat{ACM}\)= \(\widehat{DCB}\)( cx cộng vs \(\widehat{MCB}\)
BC=Ac ( gt )
=> \(\Delta ACM=\Delta BCD\left(c-g-c\right)\)
b, \(BM.BM=3cm^2\)
\(\Rightarrow BM=\sqrt{3}\)
AD t/c Pi ta- go đảo, ta có :
\(MD^2=BM^2+BD^2\)
22 = \(\left(\sqrt{3}\right)^2+1^2\)
4 = 3 + 1 \(\Rightarrow\Delta MBD\)vuông
c, Xét \(\Delta BMD\)vuông tại B, ta có :
BD = \(\frac{1}{2}MD\)
\(\Rightarrow\widehat{BMD}\)= 30o , \(\widehat{CMD}\)= 60o ( vì \(\Delta CMD\)đều )
Ta có : \(\widehat{BMD}\)+ \(\widehat{CMD}\) = \(\widehat{BMC}\)
30o + 60o = 90o
Vì \(\Delta MDC\)đều \(\Rightarrow\widehat{MDC}\)= 60o
Ta có : \(\widehat{MBD}\)+ \(\widehat{BDM}\)+ \(\widehat{DMB}\)= 180o ( tổng 3 góc trong 1 \(\Delta\))
90o + \(\widehat{BDM}\)+ 30o = 180o
\(\widehat{BDM}\)= 60o
Mà \(\widehat{MDC}\)+ \(\widehat{BDM}\)= 60o + 60o = 120o
lại có : \(\Delta CAM=\Delta CBD\)(câu a ) => \(\widehat{AMC}\)= 120o
Ta có : \(\widehat{AMB}\)+ \(\widehat{BMC}\)+ \(\widehat{AMC}\)= 360o
\(\widehat{AMB}\)+ 90o + 120o = 360o
\(\widehat{AMB}\)= 1500
Mà \(\widehat{AMB}\)+ \(\widehat{BMD}=150^o+30^o=180^o\)
\(\Rightarrow\widehat{AMD}\)là góc bẹt
=> A, M,D thẳng hàng
d, Xét \(\Delta BMC\)vuông
BC2 = BM2 + MC2
= \(\left(\sqrt{3}\right)^2+4\)
= 7
=> \(BC=\sqrt{7}\)
Shv có cạnh BC là \(\sqrt{7}.\sqrt{7}=7\)
19 tháng 5 2017
Tự vẽ hình nha !
Xét tam giác đều ABC có :
\(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)
Xét tam giác đều MDC có :
\(\widehat{DMC}=\widehat{MCD}=\widehat{CDM}=60^0\)
Ta có :
Góc ACB = ACM + MCB = 600
Góc MCD = MCB + BCD = 600
=> Góc ACM = Góc BCD
Xét tam giác ACM và tam giác BCD có :
AC = BC
CD = CM => tam giác ACM = tam giác BCD
Góc ACM = Góc BCD
SN
30 tháng 5 2021
kẻ đường cao BH của tam giác ABC thì BH cũng là đường cao của tam giác BCN
ta có diện tích tam giác ABC = 1/2 x BH x AC = 1/2 x BH x 10 = 24 => BH = 24/5 (cm)
=> Vậy diện tích tam giác BCN là : 1/2 x BH x CN = 1/2 x 24/5 x 2 = 24/5 (cm2)
- Mặt khác ta lại có diện tích tam giác ABN = diện tích tam giác ABC + diện tích tam giác BCN = 24 + 24/5 = 144/5 (cm2)
- kẻ đường cao NK của tam giác ABN thì NK cũng chính là đường cao của tam giác BNM
Diện tích của tam giác ABN là : 1/2 x NK x AB = 1/2 x NK x 16 = 144/5m => NK = 144/40 (cm)
Diện tích tam giác BNM là : 1/2 x NK x BM = 1/2 x 144/40 x 2 = 144/40 (cm2)
- Diện tích tứ giác BMNC = diện tích tam giác BCN + diện tích tam giác BMN = 24/5 + 144/40 = 336/40 = 8,4 (cm2)
Đáp số: 8,4 cm2
21 tháng 12 2022
a: Xét ΔABN và ΔAMC có
AB=AM
góc BAN=góc MAC
AN=AC
Do đó: ΔABN=ΔAMC
b: Gọi giao của ME với AB là D, NE với AC là F
góc AMD+góc MDA=90 độ
=>góc AMD+góc BDE=90 độ
=>góc DBE+góc BDE=90 độ
=>góc BED=90 độ
=>BN vuông góc với CM
c: BC^2+MN^2=BE^2+CE^2+ME^2+NE^2
=CN^2+BM^2
=>MN^2=7+5-3=9cm
=>MN=3cm
25 tháng 6 2021
Bài 1 :
Vì ABCD là hình vuông \(\Rightarrow\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90^0\)
\(\Rightarrow AB=BC=CD=AD=4\)cm
Áp dụng định lí pytago tam giác ADC vuông tại D ta có :
\(AC^2=AD^2+CD^2=16+16=32\Rightarrow AC=4\sqrt{2}\)cm
Vì ABCD là hình vuông nên 2 đường chéo bằng nhau AC = BD = 4\(\sqrt{2}\)cm
25 tháng 6 2021
Bài 2 :
Vì ABCD là hình chữ nhật nên \(AB=CD;AD=BC\)
Áp dụng định lí Pytago tam giác ACD vuông tại D ta có :
\(AC^2=AD^2+DC^2=27+9=36\Rightarrow AC=6\)cm
