NH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H9
HT.Phong (9A5)
CTVHS
25 tháng 10 2023
a) Do AB//HD \(\Rightarrow\widehat{BAC}=\widehat{ACH}\) (2 góc so le trong)
\(\Rightarrow\widehat{ACH}=40^o\)
b) Do HD//EG \(\Rightarrow\widehat{HCE}=\widehat{CEG}\) (2 góc so le trong)
\(\widehat{HCE}=50^o\)
Mà: \(\widehat{ACE}=\widehat{ACH}+\widehat{HCE}\)
\(\Rightarrow\widehat{ACE}=40^o+50^o=90^o\)
B1
16 tháng 9 2017
làm tương tự
Bài 1 Cho tam giác ABC có góc A= 40 độ,AB=AC.Gọi M Là trung điểm của BC tính các góc của mỗi tam giác AMB và tam giác AMC
bài làm
Bài 1:
-Vì M là trung điểm nên CM=BM
-Vì AM chung và theo GT AB=AC nên Tam giác ABM=tam giac ACM
Góc A=40 độ=>Góc MAB=MAC=20
Vì góc AMB+góc AMC=180 độ(2 góc kề bù) mà góc AMB=AMC nên AMB=AMC=90 độ(2 góc tương ứng)
=>góc ABM=góc ACM=70 độ
Vậy Góc A=Góc C=70 độ
Góc AMC=góc AMB=90 độ
Góc CAM=góc BAM=20 độ
Thanks nhá
17 tháng 3 2020
A C D H E B
Xét \(\Delta\)ADC và \(\Delta\)HDC có: ^DAC = ^DHC = 90 độ ; DC chung ; ^ACD = ^HCD (= ^DCE )
=> \(\Delta\)ADC = \(\Delta\)HDC => DA = DH (1)
Xét \(\Delta\)DHE có: ^DHE = 90 độ => DE là cạnh huyền => DH < DE (2)
Từ (1) ; (2) => DA < DE
LD
4 tháng 6 2017
Hình bạn tự vẽ.
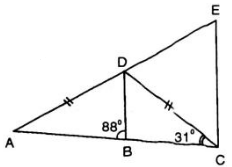
Xét \(\Delta ABC\)cân tại A ta có:
\(\widehat{DAC}=180^o-2\widehat{ACD}\)
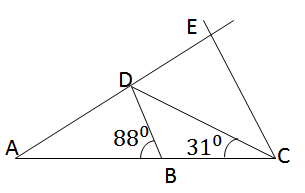
\(\widehat{DAC}=180^o-2\cdot31^o=118^o\)
Mà \(\widehat{DAC}=\widehat{ABD}+\widehat{ADB}\)( góc ngoài tại đỉnh A của \(\Delta ABD\))
Nên \(118^o=88^o+\widehat{ADB}\)
\(\Rightarrow\)\(\widehat{ADB}=118^o-88^o=30^o\)
Mặt khác \(\widehat{ADB}=\widehat{DEC}\)( 2 góc so le trong và BD // EC )
\(\Rightarrow\)\(\widehat{DEC}=30^o\)
Ta có:
\(\widehat{ACE}=\widehat{ABD}\)( 2 góc so le trong và BD // EC )
\(\widehat{ABD}=88^o\left(gt\right)\)
\(\Rightarrow\)\(\widehat{ACE}=88^o\)
Mà \(\widehat{DCE}=\widehat{ACD}+\widehat{ACE}\)
Nên \(\widehat{DCE}=31^o+88^o=119^o\)
Ta có:
\(\widehat{ACD}=\widehat{ADC}\)( \(\Delta ACD\)cân tại A)
\(\widehat{ACD}=31^o\)
\(\Rightarrow\)\(\widehat{ADC}=31^o\)
Xét \(\Delta ECD\)ta có:
\(\widehat{DCE}>\widehat{EDC}>\widehat{DEC}\left(119^o>31^o>30^o\right)\)
\(\Rightarrow\)\(ED>EC>CD\)( Quan hệ cạnh góc đối diện trong tam giác )
Vậy cạnh \(DE\)lớn nhất trong \(\Delta CDE\)
29 tháng 11 2016
cho tam giác ABC có góc A = 90 độ .kẻ AH vuông góc với BC (H thuộc BC). trên đường thẳng vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho BD=AH .chứng minh rằng
a/ tam giác AHB=tam giác DBH
b/ AB//DH
c/ tính góc ACB. biết góc BAH=35 độ
30 tháng 10 2016
Ta có hình vẽ:
A B C D H E d
Vì BD là phân giác của ABC nên \(ABD=CBD=\frac{ABC}{2}\)
Vì ABC vuông góc tại A nên góc A = 90o
Xét Δ ABC có: ABC + ACB = 90o (tính chất của Δ vuông)
=> ABC = 90o - ACB
=> \(\frac{ABC}{2}=\frac{90^o-ACB}{2}\)
=> CBD = 45o - \(\frac{ACB}{2}\)
Vì \(CH\perp DE\) nên CHD = 90o
Xét Δ BHC có: HBC + BCH = 90o (tính chất của Δ vuông)
=> 45o - \(\frac{ACB}{2}\) + BCH = 90o
=> BCH - \(\frac{ACB}{2}\) = 45o
=> BCH - \(\frac{ACB}{2}\) = \(\frac{BCE}{2}\) (vì BCE = 90o)
=> BCH \(=\frac{BCE+ACB}{2}=\frac{2.ACB+DCE}{2}=ACB+\frac{DCE}{2}\)
=> BCH - ACB = \(\frac{DCE}{2}\)
=> \(DCH=\frac{DCE}{2}\)
=> CH là tia phân giác của góc DCE (đpcm)
1 tháng 11 2016
bn ơi, bn k trả lời sớm, thầy mik chữa bài và mik nộp bài mất tiêu r 