K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 11 2019
ABCI
a) Xét tam giác ABC và tam giác DMC có :
BC = CM ( GT )
Góc ACB = góc MCD ( 2 góc đối đỉnh (
AC = CD ( GT )
=> tam giác ABC = tam giác DMC ( c - g - c )
b) Theo ý a , ta có : tam giác ABC = tam giác DMC
=> Góc BAD = góc ADM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> MD // AB ( dấu hiệu )
c) Nghĩ nốt đã
VM
27 tháng 8 2019
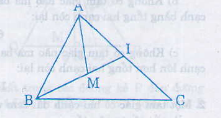
a) Ta có M nằm trong \(\Delta ABM.\)
=> \(A,M,I\) không thẳng hàng.
Theo bất đẳng thức tam giác với \(\Delta AMI\) có:
\(AM< MI+IA\left(1\right).\)
b) Cộng vào hai vế của (1) với \(MB\) ta được:
\(AM+MB< MB+MI+IA\)
Mà \(MB+MI=IB.\)
=> \(AM+MB< BI+IA.\)
c) Ta có 3 điểm \(B,I,C\) không thẳng hàng.
Theo bất đẳng thức tam giác với \(\Delta BIC\) có:
\(BI< IC+BC.\) (2)
d) Cộng vào hai vế của (2) với \(IA\) ta được:
\(BI+IA< IA+IC+BC\)
Mà \(IA+IC=AC.\)
=> \(BI+IA< AC+BC.\)
e) Vì \(\left\{{}\begin{matrix}AM+MB< BI+IA\left(cmt\right)\\BI+IA< AC+BC\left(cmt\right)\end{matrix}\right.\)
=> \(AM+MB< AC+BC.\)
Chúc bạn học tốt!
H
20 tháng 1 2020
a)Xét ΔOBC và ΔOAC có:
OC: cạnh chung
\(\widehat{BOC}=\widehat{AOC}\) (OC là phân giác góc O)
\(\widehat{OBC}=\widehat{OAC}=90^0\)
⇒ΔOBC=ΔOAC(ch−gn)
nên CA=CB(2 cạnh tương ứng)
b)Xét ΔCAD và ΔCBE có:
CA=CB(chứng minh trên)
\(\widehat{ACD}=\widehat{BCE}\) (2 góc đối đỉnh)
\(\widehat{DAC}=\widehat{EBC}=90^0\)
⇒ΔCAD=ΔCBE(cgv−gn)
nên CD=CE(2 cạnh tương ứng)
(Tự vẽ hình)
^_^
28 tháng 5 2022
a: Xét ΔABC và ΔDEC có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)
CB=CE
Do đó: ΔABC=ΔDEC
b: Ta có: ΔABC=ΔDEC
nên \(\widehat{BAC}=\widehat{EDC}=90^0\)
=>AD\(\perp\)DE
c: Xét tứ giác ABDE có
AB//DE
AB=DE
Do đó: ABDE là hình bình hành
Suy ra: BD//AE
20 tháng 2 2019
Bạn kham khảo link này nhé.
Câu hỏi của Đào Gia Khanh - Toán lớp 7 - Học toán với OnlineMath
20 tháng 2 2019
a) Xét tam giác ABC và tam giác MNC ta có:
MC=AC ( gt)
BC=NC (gt)
góc NCM = góc BCA ( 2 góc đối đỉnh )
=> tam giác ABC = tam giác MNC ( c.g.c)
b) => góc BAC = góc NMC ( 2 góc tương ứng )
<=> góc NMC=90 độ ( góc BAC=90 độ )
<=> \(AM\perp MN\)
đpcm
c) Tạo hình: gọi D là giao điểm của CE và MN
Có tam giác ABC = tam giác MNC
=> góc EBC= góc DNC ( 2 góc tương ứng )
Tự c/m: tam giác NDC = tam giác BEC ( g.c.g)
=> ND=BE ( 2 cạnh tương ứng )
tam giác AEC = tam giác MDC ( c.g.c )
=> MD=AE ( 2 cạnh tương ứng )
Lại có: AE=BE ( gt )
=> ND=MD
=> D là trung điểm của MN
=> CE đi qua trung điểm MN
đpcm
PN
26 tháng 7 2017
C A P B
a) Ta có:
\(\widehat{APC}\) là góc ngoài tại \(P\) của \(\Delta BPC\) nên \(\widehat{APC}=B+\dfrac{\widehat{C}}{2}>\dfrac{\widehat{C}}{2}=\widehat{ACP}\)
\(\Delta APC\) có:
\(\widehat{ACP}< \widehat{APC}\Rightarrow PA< CA\)
b) Ta có \(AP< CA\) (gt)
\(\Rightarrow CP< CB\)