K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
2
L
17 tháng 2 2016
a) Ta có:
\(A=\left(a-4\right)\left(a+5\right)-\left(a-5\right)\left(a+4\right)\)
\(=\left[\left(a-4\right)a+5\left(a-4\right)\right]-\left[\left(a-5\right)a+4\left(a-5\right)\right]\)
\(=\left[a^2-4a+5a-20\right]-\left[a^2-5a+4a-20\right]\)
\(=a^2-4a+5a-20-a^2+5a-4a+20\)
\(=\left(a^2-a^2\right)+\left(-4a+5a+5a-4a\right)+\left(-20+20\right)\)
\(=0+2a+0\)
\(=2a\)
L
17 tháng 2 2016
b) Ta có:
\(B=\left(2-a\right)\left(a+7\right)-\left(a-1\right)\left(a+2\right)\)
\(=\left[\left(2-a\right)a+7\left(2-a\right)\right]-\left[\left(a-1\right)a+2\left(a-1\right)\right]\)
\(=\left[2a-a^2+14-7a\right]-\left[a^2-a+2a-2\right]\)
\(=2a-a^2+14-7a-a^2+a-2a+2\)
\(=\left(2a-7a+a-2a\right)-\left(a^2+a^2\right)+\left(14+2\right)\)
\(=-6a-2a^2+16\)
LT
4
26 tháng 2 2016
(a + 1) + (a + 2) + (a + 3) + (a + 4) + (a + 5) = 115
\(\Leftrightarrow\) a + 1 + a + 2 + a + 3 + a + 4 + a + 5 = 115
\(\Leftrightarrow\) 5a + ( 1 + 2 + 3 + 4 + 5 ) = 115
\(\Leftrightarrow\) 5a + 15 = 115
\(\Leftrightarrow\) 5a = 115 - 15
\(\Leftrightarrow\) 5a = 100
\(\Leftrightarrow\) a = 100/5
\(\Leftrightarrow\) a = 20
Vậy số cần tìm là 20
26 tháng 2 2016
( a + 1 ) ( a + 2 ) + ( a + 3 ) + ( a + 4 ) + ( a + 5 ) = 115
( a x 5 ) + ( 1 + 2 + 3 + 4 + 5 ) = 115
a x 5 + 15 = 115
a x 5 = 115 - 15
a x 5 = 100
a = 100 : 5
a = 20.
DN
0
17 tháng 12 2015
\(A=\left(\frac{1-\left(\sqrt{a}\right)^3}{1-\sqrt{a}}\right)\left(\frac{1-\sqrt{a}}{1-\left(\sqrt{a}\right)^2}\right)^2\)
\(=\left(1+\sqrt{a}+a\right).\frac{1}{\left(1+\sqrt{a}\right)^2}\)
\(=\frac{1+\sqrt{a}+a}{1+2\sqrt{a}+a}\)
TM
0
NT
1
31 tháng 1 2016
\(\left(a+1\right)+\left(a+2\right)+\left(a+3\right)+\left(a+4\right)+\left(a+5\right)=115\)
\(a+1+a+2+a+3+a+4+a+5=115\)
\(\left(a+a+a+a+a\right)+\left(1+2+3+4+5\right)=115\)
\(5a+15=115\)
\(5a=115-15=100\)
\(a=\frac{100}{5}=20\)
Vậy a=20
TT
6
DT
1
CM
27 tháng 4 2017
Đáp án C
- Nhìn vào hình vẽ ta có phần thực a bị giới hạn − 2 < a < 2 , b ∈ ℝ
Chú ý: Cho số phức z = a + bi, điểm M(a;b) trong hệ trục tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z.
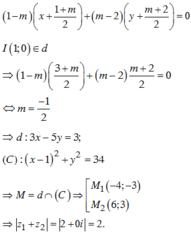
a.a=34 <=> a2=34 <=> a=\(\sqrt{34}\)
\(a.a=34\)
\(\Rightarrow\begin{cases}a=-\sqrt{34}\\a=\sqrt{34}\end{cases}\)