Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đáp án: a = 3, b = 2, c= 1, d = 5, e = 4, f = 7, g = 9, h = 8, i = 6.
ko bt đúng k nx
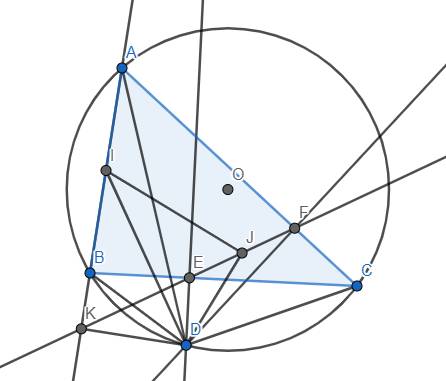
a) Theo đề bài, ta có \(\widehat{DEC}=\widehat{DFC}=90^o\) \(\Rightarrow\) Tứ giác CDEF nội tiếp do có 2 đỉnh kề nhau E, F cùng nhìn cạnh CD dưới góc vuông. \(\Rightarrow\widehat{DFE}=\widehat{DCE}=\widehat{DCB}=\widehat{DAB}\) (do tứ giác ABDC nội tiếp nên \(\widehat{DCB}=\widehat{DAB}\)). Từ đó suy ra đpcm.
b) Có \(\widehat{KBD}=\widehat{ACD}\) (do tứ giác ABDC nội tiếp) và \(\widehat{ACD}=\widehat{KED}\) (do tứ giác CDEF nội tiếp) \(\Rightarrow\widehat{KBD}=\widehat{KED}\) \(\Rightarrow\) Tứ giác DKBE nội tiếp.
Mặt khác, \(\widehat{BDA}=\widehat{BCA}=\widehat{EDF}\) và \(\widehat{BAD}=\widehat{BCD}=\widehat{EFD}\)
\(\Rightarrow\Delta DBA~\Delta DEF\left(g.g\right)\)\(\Rightarrow\dfrac{DA}{DF}=\dfrac{DB}{DE}\) \(\Rightarrow DA.DE=DB.DF\)
c) \(\Delta DBA~\Delta DEF\Rightarrow\dfrac{DB}{DE}=\dfrac{AB}{EF}=\dfrac{2BI}{2EJ}=\dfrac{BI}{EJ}\) . Lại có \(\widehat{DBI}=\widehat{DEJ}\) nên \(\Delta DBI~\Delta DEJ\left(c.g.c\right)\) \(\Rightarrow\widehat{DIB}=\widehat{DJE}\) hay \(\widehat{DIK}=\widehat{DJK}\) \(\Rightarrow\) Tứ giác DJIK nội tiếp \(\Rightarrow\) \(\widehat{DJI}=180^o-\widehat{DKI}\) . Lại có \(\widehat{DKI}=180^o-\widehat{BED}=90^o\) (do tứ giác DKBE nội tiếp) \(\Rightarrow\widehat{DJI}=90^o\) \(\Rightarrow\) đpcm

\(a,ĐK:5x\ge0\Leftrightarrow x\ge0\\ b,ĐK:3x+7\ge0\Leftrightarrow x\ge-\dfrac{7}{3}\\ c,ĐK:5-x\ge0\Leftrightarrow x\le5\\ đ,ĐK:3-2x\ge0\Leftrightarrow x\le\dfrac{3}{2}\\ f,ĐK:\dfrac{-3}{1+4x}\ge0\Leftrightarrow1+4x< 0\left(-3< 0;1+4x\ne0\right)\\ \Leftrightarrow x< -\dfrac{1}{4}\\ h,ĐK:10+x^2\ge0\Leftrightarrow x\in R\left(10+x^2\ge10>0\right)\)

Câu 1: Sai vì nếu như f(x)=ax+b(b<>0) thì f(-a)=-ax+b<>ax+b
Câu 2:
a: f(x)=0
=>-2x+1/2=0
=>-2x=-1/2
hay x=1/4
b: g(x)=-7
=>3x-1/4=-7
=>3x=-27/4
hay x=-9/4

Lời giải:
a)
\(f(x)=g(x)\Leftrightarrow 7x=2+5x^2\)
\(\Leftrightarrow 5x^2+2-7x=0\)
\(\Leftrightarrow (5x^2-5x)-(2x-2)=0\)
\(\Leftrightarrow 5x(x-1)-2(x-1)=0\Leftrightarrow (5x-2)(x-1)=0\)
\(\Rightarrow \left[\begin{matrix} x=\frac{2}{5}\\ x=1\end{matrix}\right.\)
b)
Ta có: \(\left\{\begin{matrix} f(-x)=7(-x)=-7x\\ -f(x)=-7x\end{matrix}\right.\Rightarrow f(-x)=-f(x)\)
\(\left\{\begin{matrix} g(-x)=2+5(-x)^2=2+5x^2\\ g(x)=2+5x^2\end{matrix}\right.\Rightarrow g(-x)=g(x)\)
c)
Xét \(x_1< x_2< 0\) đều thuộc TXĐ:
Khi đó:
\(g(x_1)-g(x_2)=2+5x_1^2-(2+5x_2^2)=5x_1^2-5x_2^2=5(x_1-x_2)(x_1+x_2)\)
Vì \(x_1< x_2< 0\Rightarrow x_1-x_2< 0; x_1+x_2< 0\)
Do đó: \(g(x_1)-g(x_2)=5(x_1-x_2)(x_1+x_2)>0\Rightarrow g(x_1)> g(x_2)\)
Vậy hàm số nghịch biến khi $x< 0$
------------
Xét \(x_1> x_2>0\) thuộc TXĐ:
Khi đó:
\(g(x_1)-g(x_2)=(2+5x_1^2)-(2+5x_2^2)=5x_1^2-5x_2^2=5(x_1-x_2)(x_1+x_2)\)
Vì \(x_1> x_2>0\Rightarrow x_1-x_2>0; x_1+x_2>0\)
\(\Rightarrow g(x_1)-g(x_2)>0\Rightarrow g(x_1)> g(x_2)\)
Vậy hàm số đồng biến khi $x>0$