Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Đặt \(c_1=a_1-b_1;c_2=a_2-b_2;...;c_5=a_5-b_5\)
Xét tổng \(c_1+c_2+c_3+c_4+c_5\) ta có:
\(c_1+c_2+c_3+c_4+c_5\)
\(=\left(a_1-b_1\right)+\left(a_2-b_2\right)+...+\left(a_5-b_5\right)\)
\(=0\)
\(\Rightarrow c_1;c_2;c_3;c_4;c_5\) phải có một số chẵn
\(\Rightarrow c_1.c_2.c_3.c_4.c_5⋮2\)
Vậy \(\left(a_1-b_1\right)\left(a_2-b_2\right)...\left(a_5-b_5\right)⋮2\) (Đpcm)

Đặt\(c_1=a_1-b_1,c_2=a_2-b_2,c_3=a_3-b_3,c_4=a_4-b_4,c_5=a_5-b_5\)Xét tổng \(c_1+c_2+c_3+c_4+c_5\)
Ta có:\(c_1+c_2+c_3+c_4+c_5\)=\(a_1-b_1+a_2-b_2,+a_3-b_3+a_4-b_4+a_5-b_5=0\)\(\Rightarrow\)Một trong 5 số \(c_1,c_2,c_3,c_4,c_5\) phải có 1 số chẵn
\(\Rightarrow\)\(c_1.c_2.c_3.c_4.c_5⋮2\)
\(\RightarrowĐPCM\)

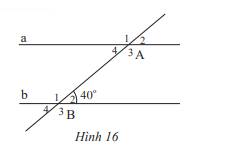
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)

a) \(A=\left(\frac{1}{2^2}-1\right)\left(\frac{1}{3^2}-1\right)\cdot\cdot\cdot\left(\frac{1}{2012^2}-1\right)\)(có 1006 số hạng nên tích của A là số dương)
\(\Rightarrow A=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)\cdot\cdot\cdot\left(1-\frac{1}{2012^2}\right)\)
\(\Rightarrow A=\left(\frac{2^2-1}{2^2}\right)\left(\frac{3^2-1}{3^2}\right)\cdot\cdot\cdot\left(\frac{2012^2-1}{2012^2}\right)\)
\(\Rightarrow A=\frac{1\cdot3}{2^2}\cdot\frac{2\cdot4}{3^2}\cdot\cdot\cdot\frac{2011\cdot2013}{2012^2}\)
\(\Rightarrow A=\text{}\frac{2013}{2\cdot2012}=\frac{2013}{4024}\)

Theo đề bài \(a_2^2=a_1a_3\) và \(a_3^2=a_2a_4\) do đó \(\frac{a_1}{a_2}=\frac{a_2}{a_3}\) và \(\frac{a_2}{a_3}=\frac{a_3}{a_4}\)
hay \(\frac{a_1}{a_2}=\frac{a_2}{a_3}=\frac{a_3}{a_4}\), suy ra \(\frac{a_1^3}{a_2^3}=\frac{a_2^3}{a_3^3}=\frac{a_3^3}{a_4^3}=\frac{a_1}{a_2}\cdot\frac{a_2}{a_3}\cdot\frac{a_3}{a_4}=\frac{a_1}{a_4}\left(1\right)\)
Mặt khác \(\frac{a_1^3}{a_2^3}=\frac{a_2^3}{a_3^3}=\frac{a_3^3}{a_4^3}=\frac{a_1^3+a_2^3+a_3^3}{a_2^3+a_3^3+a_4^3}\left(2\right)\)
Từ (1) và (2) ta có điều phải chứng minh
a) Vì A2 ở vị trí so le trong với A4
Nên A2 = A4 = 60 độ
Vì A3 ở vị trí đồng vị với A2
Nên A3 = A2 = 60 độ
Vì A1 là góc đối đỉnh của A3
Nên A3 = A1 = 60 độ
Vì B1 là trong cùng phía bù nhau với A4
Nên B1 + A4 = 180 độ
=> B1 + 60 độ = 180 độ
=> B1 = 180 -60 = 120 độ
Vì B3 là góc đối đỉnh của B1
Nên B3 = B1 = 120 độ
Vì B4 là góc đối đỉnh của B2
Nên B4 = B2 = 60 độ
b) Vì A3 và B2 ở vị trí trong cùng phía bù nhau
Nên A3 + B2 = 180 độ
A1 + B1 = 60 độ + 120 độ = 180 độ
CHÚC BẠN HỌC TỐT