
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Với mọi \(k\ge2\) thì \(\frac{2k+\sqrt{k^2-1}}{\sqrt{k-1}+\sqrt{k+1}}=\frac{\left[\left(\sqrt{k-1}\right)^2+\left(\sqrt{k+1}\right)^2+\sqrt{\left(k-1\right)\left(k+1\right)}\right]\left(\sqrt{k+1}-\sqrt{k-1}\right)}{\left(\sqrt{k-1}+\sqrt{k+1}\right)\left(\sqrt{k+1}-\sqrt{k-1}\right)}\)
\(=\frac{\sqrt{\left(k+1\right)^3}-\sqrt{\left(k-1\right)^3}}{2}\)
Suy ra tổng đã cho có thể viết là :
\(A=\frac{1}{2}\left[\sqrt{3^3}-\sqrt{1^3}+\sqrt{4^3}-\sqrt{2^3}+\sqrt{5^3}-\sqrt{3^3}+\sqrt{6^3}-\sqrt{4^3}+...+\sqrt{101^3}-\sqrt{99^3}\right]\)
\(=\frac{1}{2}\left[-1-\sqrt{2^3}+\sqrt{101^3}+\sqrt{100^3}\right]\)
\(=\frac{999+\sqrt{101^3}-\sqrt{8}}{2}\)

Ta thấy : A =\(\frac{20^{10}+1}{20^{10}-1}>1\)
Ta có : A=\(\frac{20^{10}+1}{20^{10}-1}>\frac{20^{10}+1-2}{20^{10}-1-2}=\frac{20^{10}-1}{20^{10}-3}=B\)
Vậy A > B

Đáp án C.
Bất phương trình
⇔ 10 + 1 log 3 x - 10 - 1 log 3 x ≥ 2 3 . 3 log 3 x
⇔ 10 + 1 3 log 3 x - 10 - 1 3 log 3 x ≥ 2 3
⇒ t - 1 t ≥ 2 3
⇔ t 2 - 1 ≥ 2 3 ⇔ 3 t 2 - 2 t - 3 ≥ 0 .

Câu này không có đáp án vì thấy có hạng tử \(10:0\)là không xác định được kết quả(Một số không thể chia cho 0) nên bài làm của bạn trước là sai

Ta có : \(a=10^{\frac{1}{1-lgb}}\Leftrightarrow lga=lg10^{\frac{1}{1-lgb}}=\frac{1}{1-lgb}\)
\(\Leftrightarrow lgb=1-\frac{1}{lga}=\frac{lga-1}{lga}\left(1\right)\)
\(b=10^{\frac{1}{1-lgc}}\Leftrightarrow lgb=lg10^{\frac{1}{1-lgc}}=\frac{1}{1-lgc}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{lga-1}{lga}=\frac{1}{1-lgc}\Leftrightarrow lgc=1-\frac{lga}{lga-1}=\frac{1}{1-lga}\)
\(\Leftrightarrow10^{lgc}=10^{\frac{1}{1-lga}}\Leftrightarrow c=10^{\frac{1}{1-lga}}\Rightarrow\) Điều phải chứng minh
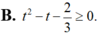
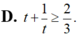
TL :
5849999977.15
~HT~
đáp án là 649999982,4
k cho mik nhé :33