NP
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 10 2019
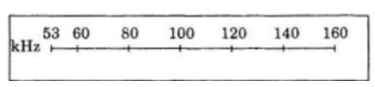
a) Theo giả thiết ta có: d = 0 => F = 53 <=> k.a0=53 <=> k = 53
Và d = 12 => F = 160 <=> k.a12=160
c) Từ câu b) => d = 25,119.lgF-43,312
(do yêu cầu kết quả tính chính xác đến hàng phần trăm)
Vậy ta có bảng.
| F | 53 | 60 | 80 | 100 | 120 | 140 | 160 |
| d | 0 | 1,35 | 4,49 | 6,93 | 8,91 | 10,60 | 12 |
18 tháng 5 2021
y=x^{2}-x-12y=x2−x−12
\Rightarrow y' = 2x-1⇒y′=2x−1.
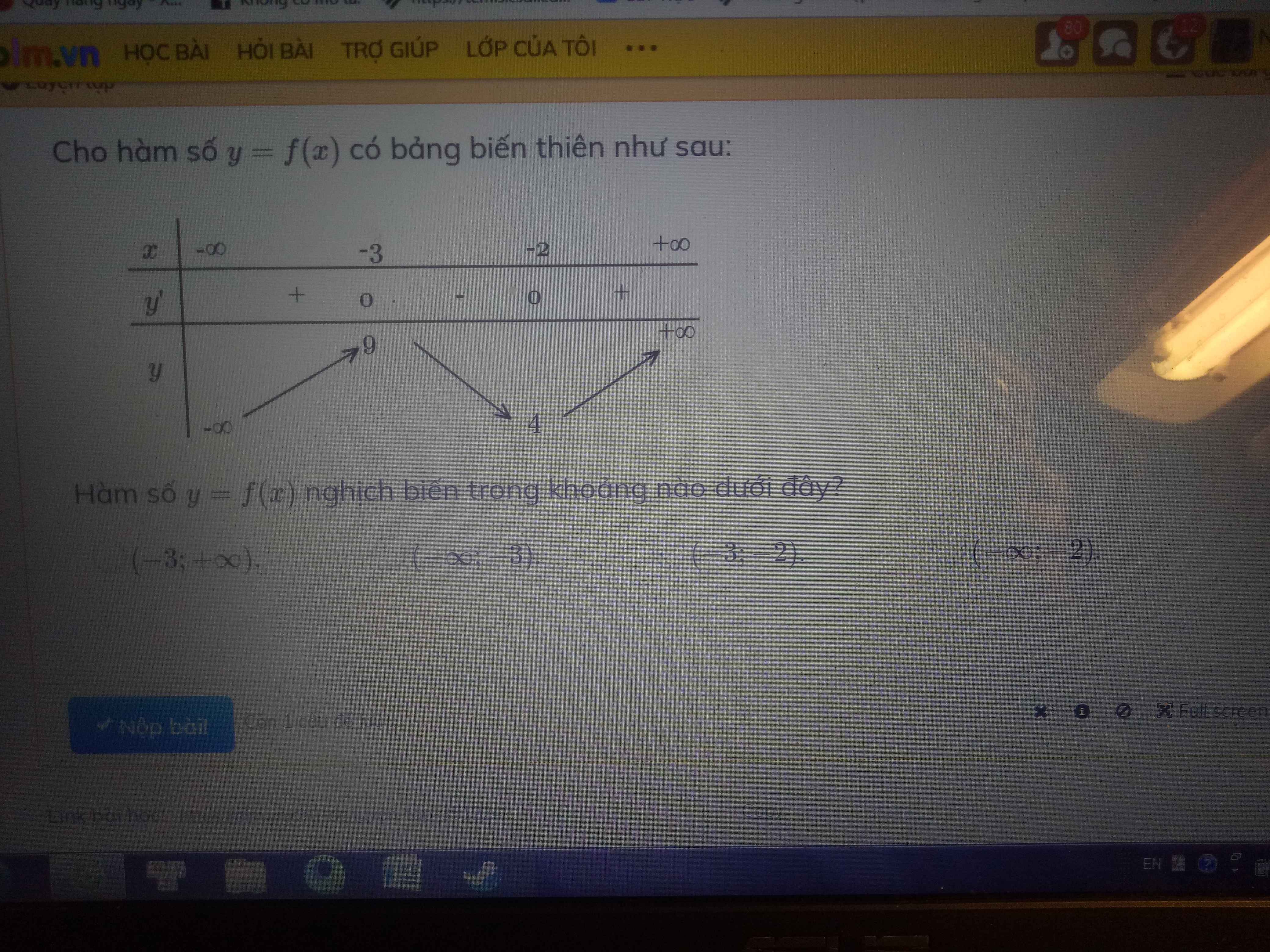
Bảng biến thiên của hàm số như sau:
xy'y-∞+∞-0-12,25>0,5>+∞+∞+-
Vậy khoảng nghịch biến của hàm số là: (-∞ ; 0,5)(−∞;0,5).
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 5 2021
Từ BBT ta thấy hàm nghịch biến trên khoảng \(\left(-3;-2\right)\)
NL
0
HQ
6 tháng 7 2021
hình như ad có sự nhầm lẫn gì đó ở đây ạ :D
chỉ nêu về sự hiểu biết của cá nhân: ad bị nhầm về trình tự làm của bài toán này mất rồi
f(|x+m|) nguyên tắc là đối xứng rồi mới tịnh tiến cơ mà ad lại đi tịnh tiến trước
qua nguyên tắc trên ta cũng rút ra được quy tắc: số điểm cực trị của y=f(|x|) cũng bằng với số điểm cực trị y=f(|x+m|) cụ thể ở bài toán là bằng 3
AH
Akai Haruma
Giáo viên
6 tháng 7 2021
Lời giải:
Theo đồ thị thì $f(x)$ đạt cực trị tại $x=-2$ và $x=4$. Ta biết rằng dạng đồ thị hàm số $y=f(|x|)$ thì ta giữ nguyên phần đồ thị nằm bên phải trục tung, sau đó lấy đối xứng qua trục tung phần đồ thị bên phải.
Vậy ở bên phải trục tung ta đã có cực trị tại $x=4$ rồi thì lấy đối xứng qua trục tung ta có thêm 1 cực trị nữa. Thêm 1 cực trị tại $x=0$ (do tính đối xứng 2 bên tạo nên). Nên tổng cộng đồ thị $f(|x|)$ có 3 cực trị.
Tịnh tiến sang phải 3 đơn vị, ta có đồ thị hàm số $f(|x-3|)$ nên đồ thị $f(|x-3|)$ cũng có 3 cực trị tại $x=-1; x=3; x=7$
Đáp án C.
OT
7
7 tháng 9 2019
Vì 1+1=1\(\times\)(1+1)=1\(\times\)2=2
k mình nha
29 tháng 1 2022
a: \(\widehat{xOz}=80^0+20^0=100^0\)
b: \(\widehat{zOm}=\dfrac{\widehat{yOz}}{2}=10^0\)
\(\Leftrightarrow\widehat{xOm}=90^0\)
tưởng học cái này từ lớp 4 r?
345,325