K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TD
5
16 tháng 10 2020
Bài làm của ông a :))
đk: \(-\sqrt[4]{2}\le x\le\sqrt[4]{2}\)
Nếu x = 0 thay vào ta được PT không có nghiệm
Nếu x khác 0 thì ta có: \(x^2\cdot\sqrt[4]{2-x^4}=x^4-x^3+1\)
\(\Leftrightarrow x^2\cdot\sqrt[4]{2-x^4}+x^3=x^4+1\)
\(\Leftrightarrow\sqrt[4]{2-x^4}+x=x^2+\frac{1}{x^2}\)
Đến đây ta sẽ sử dụng 2 BĐT quá là quen thuộc, Cauchy và Bunyakovsky!
Áp dụng Cauchy ta được: \(x^2+\frac{1}{x^2}\ge2\)
Dấu "=" xảy ra khi: \(x^2=\frac{1}{x^2}\Leftrightarrow x^4=1\Rightarrow x^2=1\)
Mặt khác, áp dụng Bunyakovsky ta có:
\(\left(\sqrt[4]{2-x^4}\right)^2\le\left(1^2+1^2\right)\left(\sqrt{2-x^4}+x^2\right)\)
\(\Rightarrow\left(\sqrt{2-x^4}+x^2\right)\le4\left(\sqrt{2-x^4}+x^2\right)^2\le4\cdot2\cdot\left(2-x^4+x^2\right)=8\cdot2=16\)
\(\Rightarrow\sqrt[4]{2-x^4}+x\le\sqrt[4]{16}=2\)
Dấu "=" xảy ra khi: x = 1
Vậy x = 1
TT
17 tháng 10 2020
\(x^2.\sqrt[4]{2-x^4}=x^4-x^3+1\left(1\right)\)
Ta có x = 0 không là \(n_0\) của (1)
Với \(x\ne0\), Ta có
\(\left(1\right)\Leftrightarrow\sqrt[4]{2-x^4}=x^2-x+\frac{1}{x^2}\)
\(\Leftrightarrow x+\sqrt[4]{2-x^4}=x^2+\frac{1}{x^2}\left(2\right)\)
\(VP_{\left(2\right)}=x^2+\frac{1}{x^2}\ge2\)(cô si )
\(VT_{\left(2\right)}=x+\sqrt[4]{2-x^4}\le\sqrt{\left(1+1\right)\left(x^2+\sqrt{2-x^4}\right)}\le\sqrt{2\sqrt{\left(1+1\right)\left(x^2+2-x^4\right)}}\)\(=\sqrt{2.\sqrt{2.2}}=2\)
Do đó \(\left(2\right)\Leftrightarrow\hept{\begin{cases}VP_{\left(2\right)}=2\\VT_{\left(2\right)}=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\x=\sqrt[4]{2-x^4}\\x^2=\sqrt{2-x^4}\end{cases}}\Leftrightarrow x=1\)
Kết luận Vậy phương trình (1) có \(n_0\)duy nhất \(x=1\)
AH
Akai Haruma
Giáo viên
1 tháng 1 2017
Câu 1:
Ta có \(\int \frac{dx}{x^4+1}=\frac{1}{2}\int \left ( \frac{x^2+1}{x^4+1}-\frac{x^2-1}{x^4+1} \right )dx=\frac{1}{2}\int \frac{1+\frac{1}{x^2}}{x^2+\frac{1}{x^2}}dx+\frac{1}{2}\int \frac{1-\frac{1}{x^2}}{x^2+\frac{1}{x^2}}dx\)
\(\frac{1}{2}\int \frac{d\left ( x-\frac{1}{x} \right )}{x^2+\frac{1}{x^2}}+\frac{1}{2}\int \frac{d\left ( x+\frac{1}{x} \right )}{x^2+\frac{1}{x^2}}=\frac{1}{2}\int \frac{d(x-\frac{1}{x})}{(x-\frac{1}{x})^2+2}+\frac{1}{2}\int \frac{d(x+\frac{1}{2})}{(x+\frac{1}{x})^2-2}\)
Đặt \(x-\frac{1}{x}=a,x+\frac{1}{x}=b\Rightarrow A=\frac{1}{2}\int \frac{da}{a^2+2}+\frac{1}{2}\int \frac{db}{b^2-2}\)
Bằng cách đặt \(a=\sqrt{2}\tan u (-\frac{\pi}{2}< u<\frac{\pi}{2})\)
\(\Rightarrow \frac{1}{2}\int \frac{da}{a^2+2}=\frac{\sqrt{2}}{4}\tan^{-1}\left (\frac{a}{\sqrt{2}} \right)+c\)
\(\frac{1}{2}\int \frac{db}{b^2-2}=\frac{1}{4\sqrt{2}}\int \left (\frac{1}{b-\sqrt{2}}-\frac{1}{b+\sqrt{2}} \right)db\)\(=\frac{1}{4\sqrt{2}}\ln|\frac{b-\sqrt{2}}{b+\sqrt{2}}|+c\)
\(\Rightarrow A=\frac{1}{2\sqrt{2}}\tan^{-1} \left (\frac{x^2-1}{\sqrt{2}x} \right)-\frac{1}{4\sqrt{2}}\ln|\frac{x^2-\sqrt{2}x+1}{x^2+\sqrt{2}x+1}|+c\)
Awn, chúc mừng năm mới!
AH
Akai Haruma
Giáo viên
1 tháng 1 2017
Câu 2:
\(B=\int \frac{x^4+1}{x^6+1}=\int\frac{(x^2+1)^2-2x^2}{(x^2+1)(x^4-x^2+1)}dx=\int\frac{x^2+1}{x^4-x^2+1}dx-2\int \frac{x^2dx}{(x^3)^2+1}\)
\(\int\frac{1+\frac{1}{x^2}}{x^2-1+\frac{1}{x^2}}dx-\frac{2}{3}\int\frac{d(x^3)}{(x^3)^2+1}=\int\frac{d\left (x-\frac{1}{x} \right)}{\left (x-\frac{1}{x}\right)^2+1}-\frac{2}{3}\int\frac{d(x^3)}{(x^3)^2+1}\)
Đặt \(x-\frac{1}{x}=a, x^3=b\). Cần tính \(B=\int\frac{da}{a^2+1}-\frac{2}{3}\int\frac{db}{b^2+1}\)
Đến đây bài toán trở về dạng quen thuộc . Đặt \(a=\tan u, b=\tan v\)
\(\Rightarrow B=\tan ^{-1}\left (x-\frac{1}{x}\right)-\frac{2}{3}\tan^{-1}(x^3)+c\)
N
1
7 tháng 9 2018
70-5(x-3)=45
5(x-3)=70-45=25
x-3=25:5
x=5 cảm ơn tao đi chúc may mắn mấy nhóc
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Đặt \(\dfrac{x}{y}+\dfrac{y}{x}=t\Rightarrow\left|t\right|\ge2\)
\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}=t^2-2\)
\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}=\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)^2-2=\left(t^2-2\right)^2-2=t^4-4t^2+2\)
\(\Rightarrow P=f\left(t\right)=t^4-4t^2+2-\left(t^2-2\right)+t\)
\(f\left(t\right)=t^4-5t^2+t+4\)
Xét hàm \(f\left(t\right)=t^4-5t^2+t+4\) trên \((-\infty;-2]\cup[2;+\infty)\)
\(f'\left(t\right)=g\left(t\right)=4t^3-10t+1\)
\(g\left(t\right)\) bậc 3 nên có tối đa 3 nghiệm
\(g\left(-2\right)=-11\) ; \(g\left(0\right)=1\)
\(\Rightarrow g\left(-2\right).g\left(0\right)< 0\Rightarrow g\left(t\right)=0\) có nghiệm \(t_1\in\left(-2;0\right)\)
\(g\left(1\right)=-5< 0\Rightarrow g\left(0\right).g\left(1\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_2\in\left(0;1\right)\)
\(g\left(2\right)=13\Rightarrow g\left(1\right).g\left(2\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_3\in\left(1;2\right)\)
Dấu \(f'\left(t\right)\):
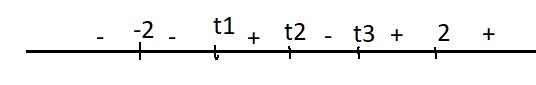
Từ đây ta thấy \(f\left(t\right)\) nghịch biến trên \((-\infty;-2]\) và đồng biến trên \([2;+\infty)\)
Hay GTNN của \(f\left(t\right)\) sẽ rơi vào \(t=-2\) hoặc \(t=2\)
\(f\left(-2\right)=-2\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(t\right)_{min}=-2\) khi \(t=-2\) hay \(P_{min}=-2\) khi \(x=-y\)
TG
1
29 tháng 3 2016
a) Chia 2 vế của phương trình cho \(5^x>0\), ta có :
\(\left(\frac{3}{5}\right)^x+\left(\frac{4}{5}\right)^x=1\)
Xét \(f\left(x\right)=\left(\frac{3}{5}\right)^x+\left(\frac{4}{5}\right)^x\)
Ta có :
\(f'\left(x\right)=\left(\frac{3}{5}\right)^x\ln\frac{3}{5}+\left(\frac{4}{5}\right)^x\ln\frac{4}{5}<0\) với mọi x
Do đó \(f\left(x\right)\) đồng biến trên R
Mặt khác
f(2) =1. Do đó x=2 là nghiệm duy nhất của phương trình
b) Phương trình tương đương với
\(2^x\left(2-2^x\right)=x-1\)
Với x=1 thì phương trình trên đúng, do đó x=1 là nghiệm của phương trình
- Nếu x>1 thì \(2<2^x\) và \(x-1>0\) do đó \(2^x\left(2-2^x\right)<0\)< \(x-1\)
phương trình vô nghiệm
- Nếu x<1 thì \(2>2^x\) và \(x-1<0\) do đó \(2^x\left(2-2^x\right)>0\)> \(x-1\)
phương trình đã cho có 1 nghiệm duy nhất là x=1
MN
0
9,876 x 4 = 9,876 : 1 x 4