
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


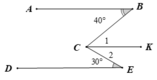
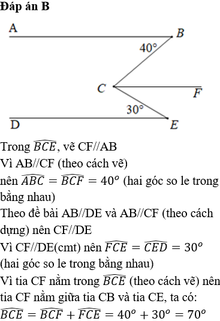
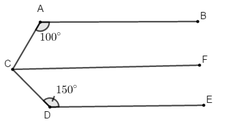
Kẻ CK // AB .Ta có AB / / CK ⇒ C ^ 1 = B ^ = 40 0 ( hai góc so le trong )
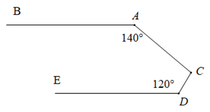
CK // AB DE // AB ⇒ CK // DE
CK / / DE ⇒ C ^ 2 = E ^ = 30 0 ( hai góc so le trong )
Do đó C 1 ^ + C 2 ^ = 40 0 + 30 0 = 70 0 ⇒ B C E ^ = 70 0

phần còn lại thì chứng minh CH với DE song song nhau theo giả thiết

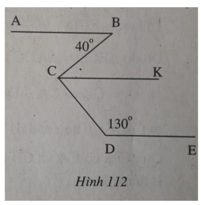
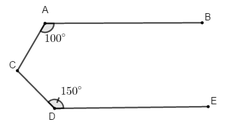
Kẻ CK // AB. Do CK // AB, DE // AB nên CK // DE.
AB // CK ⇒ ∠BCK = ∠B = 40° (so le trong)
CK // DE ⇒ ∠DCK + ∠CDE = 180° ( hai góc trong cùng phía bù nhau )
⇒ ∠DCK = 180° - ∠CDE = 180° - 130° = 50°.
Do đó: ∠BCD = ∠BCK + ∠DCK = 40° + 50° = 90°.

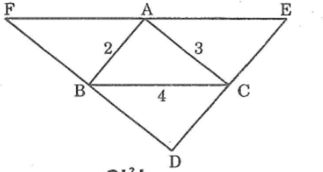
Xét ΔABC và ΔABF, ta có:
∠(ABC) =∠(BAF) (so le trong)
AB cạnh chung
∠(BAC) =∠(ABF) (so le trong)
Suy ra: ΔABC= ΔBAF(g.c.g)
Suy ra: AF = BC = 4 (hai cạnh tương ứng)
BF = AC = 3(hai cạnh tương ứng)
Xét ΔABC và ΔCEA, ta có:
∠(ACB) =∠(CAE) (so le trong)
AC cạnh chung
∠(BAC) =∠(ECA) (so le trong)
Suy ra: ΔABC= ΔCEA(g.c.g)
Suy ra: AE = BC = 4(hai cạnh tương ứng)
CE = AB = 2 (hai cạnh tương ứng)
Xét ΔABC và ΔDCB, ta có:
∠(ACB) =∠(DBC) (so le trong)
BC cạnh chung
∠(ABC) =∠(DCB) (so le trong)
Suy ra: ΔABC= ΔDCB(g.c.g)
Suy ra: DC = AB = 2(hai cạnh tương ứng)
DB = AC = 3 (hai cạnh tương ứng)
Ta có: EF = AE + AF = 4 + 4=8
DF = DB + BF = 3+ 3 =6
DE = DC + CE = 2 + 2 = 4
Vậy chu vi ΔDEF là:
DE + DF + EF = 4+ 6 + 8 =18 (đơn vị độ dài)


a) Ta có DE // AB nên D E C ^ = A ^ (cặp góc đồng vị); DF // AC nên B F D ^ = A ^ (cặp góc đồng vị).
Mặt khác B F D ^ = F D E ^ (so le trong của DE // AB)
Suy ra A ^ = D E C ^ = B F D ^ = F D E ^ .
b) Ta có D 2 ^ = B ^ (cặp góc đồng vị của DE // AB); D 1 ^ = C ^ (cặp góc so le trong của DF // AC);
Do đó D 1 ^ + D 2 ^ = B ^ + C ^ = 110 ° . Suy ra F D E ^ = 180 ° − 110 ° = 70 ° .
Vậy A ^ = 70 ° (vì A ^ = F D E ^ ).




tính góc gì thế bạn
ACD^ ah