Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải thích: Đáp án D
Phương pháp :
Sử dụng lí thuyết về dao động điều hoà kết hợp ki ̃năng đọc đồ thị viết phương trình của x
Thay t vào phương trình của v
Cách giải :
Ta có: 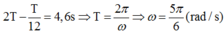
Phương trình dao động: 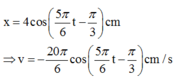
Thay t = 3s vào phương trình v ta thu được: v = -5,24 cm/s

Giải thích: Đáp án A
Phương pháp: Dựa vào đồ thị viếṭ được phương trình của li đô ̣x
Phương trình của vận tốc: v = x’
Cách giải:
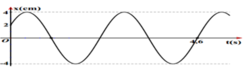
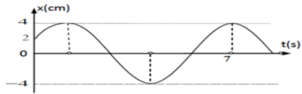
Dựa vào đồ thị ta có tại t = 0, vật ở li độ x = 2 cm và đi theo chiều dương nên pha ban đầu là – π/3
Từ vòng tròn lượng giác kết hợp với đồ thị ta được: 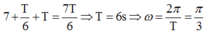
Phương trình dao động: 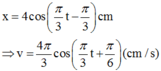

Đáp án B
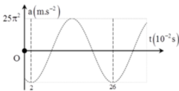
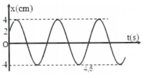
Từ đồ thị ta có: T 2 = 1,1 – 0,3 = 0,8 (s) ð T = 1,6 s
ð w = 2 π t = 2 π 1 , 6 = 1,25π (rad/s); thời điểm t = 0,7 s thì
x = -A=Acos(1,25π.0,7 + j) ð cos(1,25π.0,7 + j) = - 1 = cosπ
ð j = π – 0,785π = π 8 ; thời điểm t = 0,2 s thì x = 2 = Acos(1,25π.0,2 + π 8 )
ð A = 5,226 (cm); thời điểm t = 0,9 s thì
a = - w2x = - (1,25π)2.5,226.cos(1,25π.0,9 + π 8 ) = 56,98679 (cm/s2).
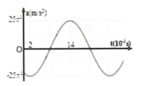



Theo đồ thị ta có: `v_[max]=8 \pi (cm//s)`
`@T/2 = 0,25.2=0,5(s)=>\omega =2\pi (rad//s)`
`=>A=[v_[max]]/[\omega]=4(cm)`
`@t=0` thì `v= 8\pi=>` Vật ở vị trí cân bằng và chuyển động theo chiều dương.
`=>\varphi = -\pi/2`
`=>` Ptr dao động: `x=4cos(2\pi t-\pi/2)`