
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(7x=3y\Rightarrow\)\(\frac{x}{3}=\frac{y}{7}\)
Đặt \(\frac{x}{3}=\frac{y}{7}=k\Rightarrow x=3k;y=7k\)
Có: x.y=84
\(\Rightarrow3k\cdot7k=84\)
\(\Rightarrow k^2=4\Rightarrow\left[\begin{array}{nghiempt}k=2\\k=-2\end{array}\right.\)
Với k=2 thì x=6 ;y=14
Với k=-2 thì x=-6 ;y =-14
b) \(7x=3y\Rightarrow\)\(\frac{x}{3}=\frac{y}{7}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có:
\(\frac{x}{3}=\frac{y}{7}=\frac{5y-2x}{5\cdot7-2\cdot3}=\frac{-4}{29}\)
=> \(\begin{cases}x=-\frac{12}{29}\\y=-\frac{28}{29}\end{cases}\)
c) \(2x=3y=5z\)
\(\Leftrightarrow\)\(\frac{2x}{30}=\frac{3y}{30}=\frac{5z}{30}\)
=> \(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}\)
Áp dụng tc của dãy tỉ số bằng nhau ta co:
\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x+2y-3z}{15+2\cdot10-3\cdot6}\)
thiếu đề
\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x+2y-3z}{15+2\cdot10-3\cdot6}=\frac{10}{17}\)
=>\(\begin{cases}x=\frac{150}{17}\\y=\frac{100}{17}\\z=\frac{60}{17}\end{cases}\)
@VỘI VÀNG QUÁ

Áp dụng TCDTSBN:
\(\dfrac{x}{7}=\dfrac{y}{3}=\dfrac{x-y}{7-3}=\dfrac{16}{4}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=28\\y=12\end{matrix}\right.\)
Nhầm ròi iem ơi :>>
\(7x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{7}\)

a.
\(\dfrac{x}{2}=\dfrac{y}{5}\Rightarrow5x-2y=0\left(1\right)\\ x+y=-21\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}x=-6\\y=-15\end{matrix}\right.\)
b,
\(7x-3y=0\left(1\right)\\ x-y=16\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}x=-12\\y=-28\end{matrix}\right.\)

7x=3y => \(\frac{x}{3}\)= \(\frac{y}{7}\)= \(\frac{x-y}{3-7}\)=\(\frac{16}{-4}\)= -4
=> x= -4 x 3= -12
y= -4 x 7= -28

a.
$7x-2y=5x-3y$
$\Leftrightarrow 2x=-y$. Thay vào điều kiện số 2 ta có:
$-y+3y=20$
$2y=20$
$\Rightarrow y=10$.
$x=\frac{-y}{2}=\frac{-10}{2}=-5$
b.
$2x=3y\Rightarrow \frac{x}{3}=\frac{y}{2}$
$3y=4z-2y\Rightarrow 5y=4z\Rightarrow \frac{y}{4}=\frac{z}{5}$
$\Rightarrow \frac{x}{6}=\frac{y}{4}=\frac{z}{5}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{6}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{6+4+5}=\frac{45}{15}=3$
$\Rightarrow x=6.3=18; y=4.3=12; z=5.3=15$

\(\frac{x}{6}=\frac{y}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau :
\(\Rightarrow\frac{x}{6}=\frac{y}{9}=\frac{x-y}{6-9}=\frac{30}{-3}=-10\)
\(\Rightarrow\frac{x}{6}=-10\Rightarrow x=-60\)
\(\frac{y}{9}=-10\Rightarrow y=-90\)

Từ giả thiết 7x = 3y 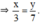
Theo tính chất của dãy tỉ số bằng nhau ta có: 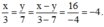
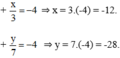
Vậy x = -12 và y = -28.

`7x=3y`
`=>x/y=3/7`
`=>x/3=y/7`
Mà `x-y=10` nên áp dụng dãy tỉ số bằng nhau ta có
`x/3=y/7=(x-y)/(3-7)=10/(-4)=-5/2`
`=>x/3=-5/2=>x=-15/2`
`=>y/7=-5/2=>y=-35/2`
7x = 3y => x/3 = y/7 và x - y = 16
Áp dụng tính chất dãy tỉ số bằng nhau, có:
\(\frac{x}{3}=\frac{y}{7}=\frac{x-y}{3-7}=\frac{16}{-4}=-4\)
Suy ra: \(\frac{x}{3}=-4\Rightarrow x=-4\cdot3=-12\)
\(\frac{y}{7}=-4\Rightarrow y=-4\cdot7=-28\)
Vậy x = -12; y = -28