Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài 1 : a) oh là tia đối oz \(\Rightarrow\) zoh thẳng hàng
ot là tia đối của tia ox \(\Rightarrow\) xot thẳng hàng
ta có : xoz = \(\dfrac{100}{2}=50^0\) (oz là tia phân giác của góc xoy)
mà xoz = toh (đối đỉnh) \(\Rightarrow\) toh = 500
b) ta có : toh = xoz (đối đỉnh)
mà toh = 400 \(\Rightarrow\) xoz = 400
\(\Rightarrow\) xoy = 40.2 = 800
bạn ơi tớ bảo phần ab bài 1 tớ biết làm rồi tớ muốn cậu có thể giúp tớ bài 2 và bài 3,bài 1 c,d được không
xin cảm ơn các bạn trước!

Xét 2 t.h là ra mà bn : a âm - b dương
a dương -b âm ( loại vì thế k thỏa mãn bài )
minhf cũng làm theo cach này nhưng cô bảo là chưa chắc đã dc điểm![]()

Vì \(b\ne d;b+d\ne0\) nên áp dụng tính chất cảu dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\)
Vậy \(\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\) (đpcm)
Chúc bạn học tốt!!!
Ta có:Nếu
\(\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\)
thì \((a+c)(b-d)=(a-c)(b+d)\)
\(a(b-d)+c(b-d)=a(b+d)-c(b+d)\)
\(ab-ad+bc-cd=ab+ad-bc+cd\)
\(=\)\(ab-ab\)\(-ad+ad\)\(+bc-bc\)\(-cd+cd\)
\(=0\)
\(\Leftrightarrow\left(a+c\right)\left(b-d\right)\)\(=\left(a-c\right)\left(b+d\right)\)
\(\Leftrightarrow\dfrac{a+c}{b+d}\)\(=\dfrac{a-c}{b-d}\)

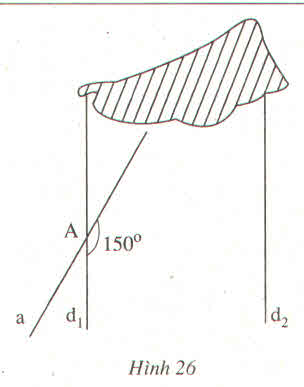
Ta có : ˆA1A1^ và ˆA2A2^ là hai góc kề bù nên:
ˆA1+ˆA2=1800⇒ˆA2=1800−ˆA1=1800−1500=300A1^+A2^=1800⇒A2^=1800−A1^=1800−1500=300
Vì d1 // d2 và ˆA2A2^ so le trong với ˆB1B1^
⇒ˆB1=ˆA2=300⇒B1^=A2^=300
Vậy ˆB1=300
Gọi B giao điểm của a và d2.
d1 // d2 nên góc nhọn tại B bằng góc nhọn tại A và bằng
1800 - 1500= 300.

a.Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\) (1)
\(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\dfrac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2) suy ra: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
b.M = \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{50^2}\right)\)
= \(\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}\)
= \(\dfrac{1.3.2.4.3.5...49.51}{2^2.3^2.4^2...50^2}\)
\(\dfrac{51}{2.50}=\dfrac{51}{100}\)
Lời giải:
a)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow \left(\frac{a}{b}\right)^2=\left(\frac{b}{d}\right)^2=\frac{(a+c)^2}{(b+d)^2}(1)\)
Mặt khác, \(\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}(2)\) (áp dụng tính chất dãy tỉ số bằng nhau)
Từ \((1),(2)\Rightarrow \frac{(a+c)^2}{(b+d)^2}=\frac{a^2+c^2}{b^2+d^2}\)
b) Vì \(1-\frac{1}{2^2};1-\frac{1}{3^2};...;1-\frac{1}{50^2}<1\) nên:
\(\left\{\begin{matrix} \left \{ 1-\frac{1}{2^2} \right \}=1-\frac{1}{2^2}\\ \left \{ 1-\frac{1}{3^2} \right \}=1-\frac{1}{3^2}\\ ....\\ \left \{ 1-\frac{1}{50^2} \right \}=1-\frac{1}{50^2}\end{matrix}\right.\)
\(\Rightarrow M=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)....\left(1-\frac{1}{50^2}\right)\)
\(\Leftrightarrow M=\frac{(2^2-1)(3^2-1)(4^2-1)....(50^2-1)}{(2.3....50)^2}\)
\(\Leftrightarrow M=\frac{[(2-1)(3-1)...(50-1)][(2+1)(3+1)...(50+1)]}{(2.3.4...50)^2}\)
\(\Leftrightarrow M=\frac{(2.3...49)(3.4.5...51)}{(2.3.4...50)^2}=\frac{(2.3.4...49)^2.50.51}{2.(2.3....49)^2.50^2}=\frac{50.51}{2.50^2}=\frac{51}{100}\)

tính biểu thức A đầu tiien cậu tìm số số hạng nhé : 240-20/1=220 (cậu hiểu 1 là khoảng cách giữa 2 số liền nhau trong dãy) rồi cậu tính (240+20).220/2= thui cậu tự bấm máy nhé mẹ mình cùm mt của mình đi dạy rùi nhớ like nhé bạn tên đẹp![]()
cảm ơnnnnnnnnnnnnnnnnnnnn nhìu đúng là tên đẹp có khác like cái nữa đi![]()

Ta có:
\(A=2^0+2^1+2^2+...+2^{40}\)
\(\Rightarrow A=1+2+2^2+...+2^{40}\)
\(\Rightarrow2A=2+2^2+2^3+...+2^{41}\)
\(\Rightarrow2A-A=\left(2+2^2+2^3+...+2^{41}\right)-\left(1+2+2^2+...+2^{40}\right)\)
\(\Rightarrow A=2^{41}-1\)
Vì \(2^{41}-1< 2^{41}\) nên A < B
Vậy A < B

\(a,x^2-113=31\\ \Leftrightarrow x^2=144\\ \Leftrightarrow x=\pm12\\ Vay...\\ b,\sqrt{x+2,29}=2.3\\ \Leftrightarrow x+2,29=6^2\\ x=36-2,29=33,71\\ c,x^4=256\\ \Leftrightarrow x=\pm4\\ Vay...\\ d,\left(\sqrt{x}-1\right)^2=0,5625\\ \Leftrightarrow\sqrt{x}-1\in\left\{-0,75;0,75\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{0,25;1,75\right\}\\ Vay...\\ e,2\sqrt{x}-x=0\\ \Leftrightarrow\sqrt{x}\left(2-\sqrt{x}\right)=0\\ \Leftrightarrow\sqrt{x}=0hoac2-\sqrt{x}=0\\ \Leftrightarrow x=0hoacx=4\\ f,x+\sqrt{x}=0\\ \Leftrightarrow\sqrt{x}\left(\sqrt{x}+1\right)=0\\ \Leftrightarrow x=0hoacx=1\)
a. x2−113=31
=> x2=144
=> x2=\(\sqrt{144}\)
=> x=\(\pm12\)
c.x4=256
=> x4=44
=> x=\(\pm4\)

Bảng tần số:
Đối với xạ thủ A
Đối với xạ thủ B
Đáp án cần chọn là: C