Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu 1 : Cho #Hỏi cộng đồng OLM #Toán lớp 7

Câu 1 : Cho #Hỏi cộng đồng OLM #Toán lớp 7

Câu 2:
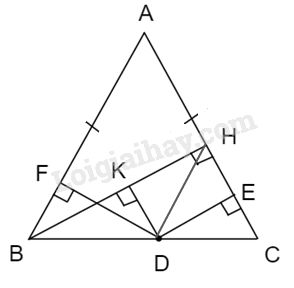
Kẻ \(DK\perp BH.\)
Mà \(BH\perp AC\left(gt\right)\)
=> \(DK\) // \(AC\) (từ vuông góc đến song song).
Hay \(DK\) // \(HC.\)
=> \(\widehat{KDB}=\widehat{HCD}\) (vì 2 góc đồng vị).
+ Vì \(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
=> \(\widehat{FBD}=\widehat{HCD}.\)
Mà \(\widehat{KDB}=\widehat{HCD}\left(cmt\right)\)
=> \(\widehat{FBD}=\widehat{KDB}.\)
Xét 2 \(\Delta\) vuông \(BFD\) và \(DKB\) có:
\(\widehat{BFD}=\widehat{DKB}=90^0\)
Cạnh BD chung
\(\widehat{FBD}=\widehat{KDB}\left(cmt\right)\)
=> \(\Delta BFD=\Delta DKB\) (cạnh huyền - góc nhọn).
=> \(DF=BK\) (2 cạnh tương ứng) (1).
Nối D với H.
+ Vì \(DK\) // \(AC\left(cmt\right)\)
=> \(DK\) // \(EH.\)
=> \(\widehat{KDH}=\widehat{EHD}\) (vì 2 góc so le trong).
Xét 2 \(\Delta\) vuông \(DEH\) và \(HKD\) có:
\(\widehat{DEH}=\widehat{HKD}=90^0\)
Cạnh DH chung
\(\widehat{EHD}=\widehat{KDH}\left(cmt\right)\)
=> \(\Delta DEH=\Delta HKD\) (cạnh huyền - góc nhọn).
=> \(DE=HK\) (2 cạnh tương ứng) (2).
Từ (1) và (2) => \(DF+DE=BK+HK.\)
Mà \(BK+HK=BH\)
=> \(DF+DE=BH\left(đpcm\right).\)
Chúc bạn học tốt!
1) Cho #Hỏi cộng đồng OLM #Toán lớp 7

1) Cho \(\Delta\)ABC có AB = AC . Lấy điểm D trên cạnh AB , Điểm E trên cạnh AC sao cho AD = AE
a) Chứng minh : BE = CD
b) Gọi O là giao điểm của BE và CD . Chứng minh rằng \(\Delta\) BOD = \(\Delta\)COE
2) Cho \(\Delta\)ABC vuông tại A. Tia phân giác của góc B cắt AC ở D . Kẻ DE vuông góc với BC . C/m rằng AB = BE

A B C O D E
a) Ta có: AD + DB = AB
AE + EC = AC
mà AB = AC; AD = AE => DB = EC
Vì AB = AC nên \(\Delta\)ABC cân tại A
=> \(\widehat{ABC}\) = \(\widehat{ACB}\) (góc đáy)
hay \(\widehat{DBC}\) = \(\widehat{ECB}\)
Xét \(\Delta\)DCB và \(\Delta\)EBC có:
DB = EC (c/m trên)
\(\widehat{DBC}\) = \(\widehat{ECB}\) (c/m trên)
BC chung
=> \(\Delta\)DCB = \(\Delta\)EBC (c.g.c)
=> DC = EB (2 cạnh tương ứng)
b) Do \(\Delta\)DCB = \(\Delta\)EBC (câu a)
=> \(\widehat{BDC}\) = \(\widehat{CEB}\) (2 góc t/ư)
hay \(\widehat{BDO}\) = \(\widehat{CEO}\)
Xét \(\Delta\)ABE và \(\Delta\)ACD có:
AE = AD (gt)
\(\widehat{A}\) chug
AB = AC (gt)
=> \(\Delta\)ABE = \(\Delta\)ACD (c.g.c)
=> \(\widehat{ABE}\) = \(\widehat{ACD}\) (2 góc t/ư)
hay \(\widehat{DBO}\) = \(\widehat{ECO}\)
Xét \(\Delta\)BOD và \(\Delta\)COE có:
\(\widehat{DBO}\) = \(\widehat{ECO}\) (c/m trên)
BD = CE (c/m trên)
\(\widehat{BDO}\) = \(\widehat{CEO}\) (c/m trên)
=> \(\Delta\)BOD = \(\Delta\)COE (g.c.g)
D E A B C O 1 2 1 2 1 1
a, xét \(\Delta\) ABE và \(\Delta\) ACD có
\(\widehat{A}\) góc chung
AE = AD (gt)
AB = AC (gt)
=> \(\Delta\) ABE = \(\Delta\) ACD (cgc) => BE = CD
b, ta có \(\widehat{D1}\) + \(\widehat{D2}\) = 180o ( kề bù )
\(\widehat{E1}\) + \(\widehat{E2}\) = 180o ( kề bù )
mà \(\widehat{D1}\) = \(\widehat{E1}\) ( \(\Delta\) ABE = \(\Delta\) ACD )
=> \(\widehat{D2}\) = \(\widehat{E2}\)
ta có AD + DB = AB
AE + EC = AC
mà AB = AC, AD = AE => DB = EC
xét Δ BOD và Δ COE có
\(\widehat{D2}\) = \(\widehat{E2}\)

20 12 5 A B C
Áp dụng định lý pytago vào \(\Delta\)ABH vuông tại H có:
AB2 = AH2 + BH2
=> AB2 = 122 + 52
=> AB2 = 169
=> AB = 13
Áp dụng định lý pytago vào \(\Delta\)ACH có:
AC2 = AH2 + CH2
=> 202 = 122 + CH2
=> CH2 = 202 - 122
=> CH2 = 256
=> CH = 16
Ta có: BC = BH + CH
= 5 + 16 = 21
Lại có: AB = 13
BC = 21
AC = 20
=> 13 + 20 \(\ne\) 21
Áp dụng định lý pytago đảo => \(\Delta\)ABC là tgv.
ờm, bn cho mk sửa cái đoạn kết luận là abc ko phải là tgv nhé

Hình vẽ:
A B C E D 1 2
Giải:
a) Xét tam giác ABD và tam giác AED, ta có:
\(\widehat{A_1}=\widehat{A_2}\) (AD là tia phân giác của góc A)
AD là cạnh chung
\(AB=AE\left(gt\right)\)
\(\Rightarrow\Delta ABD=\Delta AED\left(c.g.c\right)\)
\(\Rightarrow DB=DE\) (Hai cạnh tương ứng)
\(\Rightarrowđpcm\)
b) Ta có:
\(AB=AE\)
Mà \(E\in AC\)
Nên để \(\Delta ABD=\Delta ADC\) thì phải thêm điều kiện \(AB=AC\)
Hay nói cách khác theo hình vẽ là \(C\equiv E\).
c) Để \(DE\perp AC\)
\(\Leftrightarrow\widehat{AED}=90^0\)
Mà \(\widehat{AED}=\widehat{ABD}\) ( \(\Delta ABD=\Delta AED\))
Nên để \(DE\perp AC\) thì phải thêm điều kiện \(\widehat{ABD}=90^0\).
Chúc bạn học tốt!

a.Cho ABC cân tại C => CA=CB
Xét ΔCHA và ΔCHB có:
CA=CB
CH chung
góc CHA=CHA=90 độ
=> ΔCHA=ΔCHB ( cạnh huyền-cạnh góc vuông)
b. ΔCHA=ΔCHB => BH=HA
mà BH+HA=BA=8
=> BH=HA=4
Xét tam giác BHC vuông tại H,ta có:
\(CH^2=BC^2-BH^2\)
=> \(CH^2=5^2-4^2\)
=> \(CH^2=9\)
=> CH=3
Hình : TỰ VẼ .
Bài làm :
Giả thiết , kết luận tự làm nhé.
a. Xét \(\Delta CHA\) và \(\Delta CHB\) , ta có :
CH cạnh chung
H = 90° (CH \(\perp\) AB)
CA = CB (gt)
=> \(\Delta CHA\) = \(\Delta CHB\) (cạnh huyền - cạnh góc vuông)
....Còn nhiều cách bài này nhưng sợ cách này không biết . Bạn có thể xem sách tập 2 để hiểu hơn về cách này nhé.
=> AH = BH (2 cạnh tương ứng)
=> AH = BH = \(\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
b. Trong \(\Delta\) CHB , có :
H = 90°
=> \(CH^2\) = \(BC^2-HB^2=5^2-4^2=9\)
=> \(CH^2=\sqrt{9}=3\) (Vì CH >0)
c.