Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 7:
a.
$A=(x-1)(x-3)+11=x^2-4x+3+11=x^2-4x+14$
$=(x^2-4x+4)+10=(x-2)^2+10\geq 10$
Vậy gtnn của $A$ là $10$ khi $x=2$
b.
$B=5-4x^2+4x=6-(4x^2-4x+1)=6-(2x-1)^2\leq 6$
Vậy gtln của $B$ là $6$ khi $2x-1=0\Leftrightarrow x=\frac{1}{2}$
c.
$x-y=2\Rightarrow x=y+2$. Khi đó:
$B=y^2-3x^2=y^2-3(y+2)^2=y^2-(3y^2+12y+12)=-2y^2-12y-12$
$=6-2(y^2+6y+9)=6-2(y+3)^2\leq 6$
Vậy $B_{\max}=6$
Bài 8:
Đặt $f(x)=x^3-3x^2+5x+a$
Theo định lý Bê-du, để $f(x)\vdots x-2$ thì $f(2)=0$
$\Leftrightarrow 6+a=0$
$\Leftrightarrow a=-6$
a: Ta có: \(A=-x^2+2x+5\)
\(=-\left(x^2-2x-5\right)\)
\(=-\left(x^2-2x+1-6\right)\)
\(=-\left(x-1\right)^2+6\le6\forall x\)
Dấu '=' xảy ra khi x=1
b: Ta có: \(B=-x^2-8x+10\)
\(=-\left(x^2+8x-10\right)\)
\(=-\left(x^2+8x+16-26\right)\)
\(=-\left(x+4\right)^2+26\le26\forall x\)
Dấu '=' xảy ra khi x=-4
c: Ta có: \(C=-3x^2+12x+8\)
\(=-3\left(x^2-4x-\dfrac{8}{3}\right)\)
\(=-3\left(x^2-4x+4-\dfrac{20}{3}\right)\)
\(=-3\left(x-2\right)^2+20\le20\forall x\)
Dấu '=' xảy ra khi x=2
d: Ta có: \(D=-5x^2+9x-3\)
\(=-5\left(x^2-\dfrac{9}{5}x+\dfrac{3}{5}\right)\)
\(=-5\left(x^2-2\cdot x\cdot\dfrac{9}{10}+\dfrac{81}{100}-\dfrac{21}{100}\right)\)
\(=-5\left(x-\dfrac{9}{10}\right)^2+\dfrac{21}{20}\le\dfrac{21}{20}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{9}{10}\)
e: Ta có: \(E=\left(4-x\right)\left(x+6\right)\)
\(=4x+24-x^2-6x\)
\(=-x^2-2x+24\)
\(=-\left(x^2+2x-24\right)\)
\(=-\left(x^2+2x+1-25\right)\)
\(=-\left(x+1\right)^2+25\le25\forall x\)
Dấu '=' xảy ra khi x=-1
f: Ta có: \(F=\left(2x+5\right)\left(4-3x\right)\)
\(=8x-6x^2+20-15x\)
\(=-6x^2-7x+20\)
\(=-6\left(x^2+\dfrac{7}{6}x-\dfrac{10}{3}\right)\)
\(=-6\left(x^2+2\cdot x\cdot\dfrac{7}{12}+\dfrac{49}{144}-\dfrac{529}{144}\right)\)
\(=-6\left(x+\dfrac{7}{12}\right)^2+\dfrac{529}{24}\le\dfrac{529}{24}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{7}{12}\)
\(B=-\left(4x^2-4x+1\right)+6=-\left(2x-1\right)^2+6\le6\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
p) \(x^3-3x^2+3x-1+2\left(x^2-x\right)\\ =\left(x^3-1\right)-\left(3x^2-3x\right)+2x\left(x-1\right)\\ =\left(x-1\right)\left(x^2+x+1\right)-3x\left(x-1\right)+2x\left(x-1\right)\\ =\left(x-1\right)\left(x^2+x+1-3x+2x\right)\\ =\left(x-1\right)\left(x^2+1\right)\)
p:Ta có: \(x^3-3x^2+3x-1+2\left(x^2-x\right)\)
\(=\left(x-1\right)^3+2x\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2-2x+1+2x\right)\)
\(=\left(x-1\right)\left(x^2+1\right)\)
\(A=-x^2+x=-\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
Dấu ''='' xảy ra khi x = 1/2
\(A=-x^2+x=-\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
Dấu '=' xảy ra khi x=1/2
\(P=\left(x^2-4x+4\right)+\left(y^2+8y+16\right)+2021\\ P=\left(x-2\right)^2+\left(y+4\right)^2+2021\ge2021\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-4\end{matrix}\right.\)
Lời giải:
$P(x)=x^2+y^2-4x+8y+2041=(x^2-4x+4)+(y^2+8y+16)+2021$
$=(x-2)^2+(y+4)^2+2021\geq 0+0+2021=2021$
Vậy $P(x)$ min = $2021$ khi $x-2=y+4=0$
$\Leftrightarrow x=2; y=-4$
a: \(5x^4-x^3+7x\)
\(=x\left(5x^3-x^2+7\right)\)
c: \(x^2-5x+6=\left(x-2\right)\left(x-3\right)\)
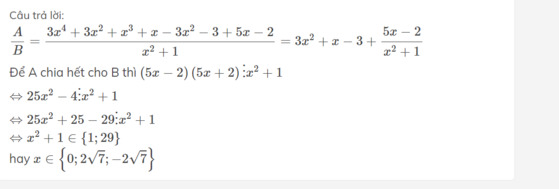
\(7,\\ a,A=x^2-4x+3+11=\left(x-2\right)^2+10\ge10\\ \text{Dấu }"="\Leftrightarrow x=2\\ b,B=-\left(4x^2-4x+1\right)+6=-\left(2x-1\right)^2+6\le6\\ \text{Dấu }"="\Leftrightarrow x=\dfrac{1}{2}\\ c,x-y=2\Leftrightarrow x=y+2\\ \Leftrightarrow B=y^2-3x^2=y^2-3\left(y+2\right)^2\\ \Leftrightarrow B=y^2-3y^2-12y-12=-4y^2-12y-12\\ \Leftrightarrow B=-\left(4y^2+12y+9\right)-3=-\left(2y+3\right)^2-3\le-3\\ \text{Dấu }"="\Leftrightarrow y=-\dfrac{3}{2}\Leftrightarrow x=\dfrac{1}{2}\)
\(8,\\ \Leftrightarrow x^3-3x^2+5x+a=\left(x-2\right)\cdot a\left(x\right)\)
Thay \(x=2\Leftrightarrow8-12+10+a=0\Leftrightarrow a=-6\)
mình thấy chưa triệt để