
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(6x^2-2x\left(3x+\dfrac{3}{2}\right)=9\)
\(\Rightarrow6x^2-6x^2-3x=9\)
\(\Rightarrow-3x=9\)
\(\Rightarrow x=\dfrac{9}{-3}\)
\(\Rightarrow x=-3\)
\(6x^2-2x\left(3x+\dfrac{3}{2}\right)=9\\ \Leftrightarrow6x^2-6x^2-3x=9\\ \Leftrightarrow3x=9\\ \Leftrightarrow x=3\)

15 \(\times\) ( 2\(x\) - 16) - (6\(x^2\) + 15\(x\)): 3\(x\) = 20
15 \(\times\) (2\(x\) - 16) - 3\(x\)( 2\(x\) + 5):3\(x\) = 20
30\(x\) - 240 - (2\(x\) + 5) = 20
30\(x\) - 240 - 2\(x\) - 5 = 20
28\(x\) - 245 = 20
28\(x\) = 20 + 245
28\(x\) = 265
\(x\) = 265:28
15(2x-16)-(6\(x^2\)+15x):3x=20
=>30x-240-2x-5=20
=>28x=265
=>x=\(\dfrac{265}{28}\)

 `6x^2-2x+1=(6x^2-2x)+1=2x(3x-1)+1`
`6x^2-2x+1=(6x^2-2x)+1=2x(3x-1)+1`
`->` Thương của phép chia `6x^2-2x+1` cho `3x-1` là `2x` và có số dư là `1`

* Trả lời:
\(\left(1\right)\) \(-3\left(1-2x\right)-4\left(1+3x\right)=-5x+5\)
\(\Leftrightarrow-3+6x-4-12x=-5x+5\)
\(\Leftrightarrow6x-12x+5x=3+4+5\)
\(\Leftrightarrow x=12\)
\(\left(2\right)\) \(3\left(2x-5\right)-6\left(1-4x\right)=-3x+7\)
\(\Leftrightarrow6x-15-6+24x=-3x+7\)
\(\Leftrightarrow6x+24x+3x=15+6+7\)
\(\Leftrightarrow33x=28\)
\(\Leftrightarrow x=\dfrac{28}{33}\)
\(\left(3\right)\) \(\left(1-3x\right)-2\left(3x-6\right)=-4x-5\)
\(\Leftrightarrow1-3x-6x+12=-4x-5\)
\(\Leftrightarrow-3x-6x+4x=-1-12-5\)
\(\Leftrightarrow-5x=-18\)
\(\Leftrightarrow x=\dfrac{18}{5}\)
\(\left(4\right)\) \(x\left(4x-3\right)-2x\left(2x-1\right)=5x-7\)
\(\Leftrightarrow4x^2-3x-4x^2+2x=5x-7\)
\(\Leftrightarrow-x-5x=-7\)
\(\Leftrightarrow-6x=-7\)
\(\Leftrightarrow x=\dfrac{7}{6}\)
\(\left(5\right)\) \(3x\left(2x-1\right)-6x\left(x+2\right)=-3x+4\)
\(\Leftrightarrow6x^2-3x-6x^2-12x=-3x+4\)
\(\Leftrightarrow-15x+3x=4\)
\(\Leftrightarrow-12x=4\)
\(\Leftrightarrow x=-\dfrac{1}{3}\)

a: \(\Leftrightarrow12x^2-10x-12x^2-28x=7\)
=>-38x=7
hay x=-7/38
b: \(\Leftrightarrow-10x^2-5x+9x^2+6x+x^2-\dfrac{1}{2}x=0\)
=>1/2x=0
hay x=0
c: \(\Leftrightarrow18x^2-15x-18x^2-14x=15\)
=>-29x=15
hay x=-15/29
d: \(\Leftrightarrow x^2+2x-x-3=5\)
\(\Leftrightarrow x^2+x-8=0\)
\(\text{Δ}=1^2-4\cdot1\cdot\left(-8\right)=33>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-1-\sqrt{33}}{2}\\x_2=\dfrac{-1+\sqrt{33}}{2}\end{matrix}\right.\)
e: \(\Leftrightarrow-15x^2+10x-10x^2-5x-5x=4\)
\(\Leftrightarrow-25x^2=4\)
\(\Leftrightarrow x^2=-\dfrac{4}{25}\left(loại\right)\)

a: =3x^3-15x^2+21x
b: =-x^3+6x^2+5x-4x^2-24x-20
=-x^3+2x^2-19x-20
c: =9x^2+15x-3x-5-7x^2-14
=2x^2+12x-19
d: =10x^2-4x+2/3
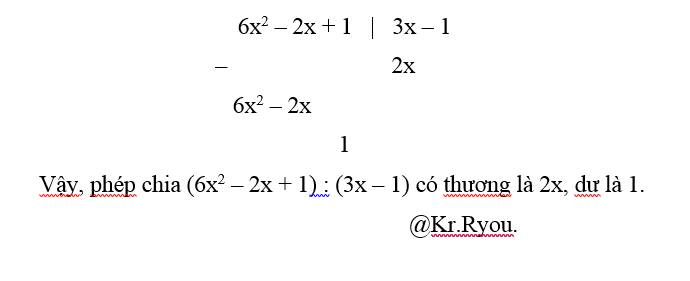
\(6x^2-\left(2x+5\right).\left(3x-2\right)=7\Leftrightarrow6x^2-\left(6x^2-4x+15x-10\right)=7\)
\(\Leftrightarrow6x^2-6x^2+4x-15x+10=7\Leftrightarrow4x-15x=7-10\)
\(\Leftrightarrow-11x=-3\Leftrightarrow x=\dfrac{-3}{-11}=\dfrac{3}{11}\) vậy \(x=\dfrac{3}{11}\)
\(6x^2-\left(2x+5\right)\left(3x-2\right)=7\)
\(\Rightarrow6x^2-2x\left(3x-2\right)-5\left(3x-2\right)=7\)
\(\Rightarrow6x^2-6x^2+4x-15x+10=7\)
\(\Rightarrow-11x+10=7\)
\(\Rightarrow-11x=-3\)
\(\Rightarrow x=\dfrac{3}{11}\)