Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 2: Cho biểu thức : A= ( #Hỏi cộng đồng OLM #Toán lớp 8

Bài 2: Cho biểu thức : A= ( #Hỏi cộng đồng OLM #Toán lớp 8



Sửa đề: Tìm GTLN của P
P = 27 - 6x - 9x²
= -(9x² + 6x + 1 - 28)
= -[(3x + 1)² - 28]
= -(3x + 1)² + 28
Do (3x + 1)² ≥ 0 với mọi x
⇒ -(3x + 1)² ≤ 0 với mọi x
⇒ -(3x + 1)² + 28 ≤ 28 với mọi x
Vậy GTLN của P là 28 khi x = -1/3

a) Ta có: \(A=\left(4-x\right)\left(16+4x+x^2\right)-\left(4-x\right)^3\)
\(=64-x^3+\left(x-4\right)^3\)
\(=64-x^3+x^3-12x^2+48x-64\)
\(=-12x^2+48x\)
b) Ta có: \(B=\left(3x+2\right)\left(9x^2-6x+4\right)-\left(3x-2\right)\left(9x^2+6x+4\right)\)
\(=27x^3+8-27x^3+8\)
=16
c) Ta có: \(C=\left(x+1\right)\left(x^2-x+1\right)-x\left(x+1\right)^2\)
\(=x^3+1-x\left(x^2+2x+1\right)\)
\(=x^3+1-x^3-2x^2-x\)
\(=-2x^2-x+1\)


a) \(\left(3x-2\right)\left(9x^2+6x+4\right)-\left(3x-1\right)\left(9x^2-3x+1\right)=x-4\)
\(\Leftrightarrow\left(3x-2\right)\left[\left(3x\right)^2+3x\cdot2+2^2\right]-\left(3x-1\right)\left[\left(3x\right)^2+3x\cdot1+1\right]=x-4\)
\(\Leftrightarrow\left(3x\right)^3-2^3-\left[\left(3x\right)^3-1\right]=x-4\)
\(\Leftrightarrow x=-3\) ( thỏa mãn )
P/s : Đề câu b) viết lại nhé, mình không hiểu lắm :))
\(9\left(2x+1\right)=4\left(x-5\right)^2\)
\(\Leftrightarrow18x+9=4\left(x^2-10x+25\right)\)
\(\Leftrightarrow18x+9=4x^2-40x+100\)
\(\Leftrightarrow4x^2-58x+91=0\)
Ta có \(\Delta=58^2-4.4.91=1908,\sqrt{\Delta}=6\sqrt{53}\)
\(\Rightarrow x=\frac{58\pm6\sqrt{53}}{8}\)
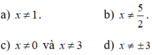
mk nghĩ bạn làm đúng rồi đó
Chắc đúng