
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có thể giúp em được không ạ, em không hiểu ạ. Em xin lỗi và cảm ơn ạ.

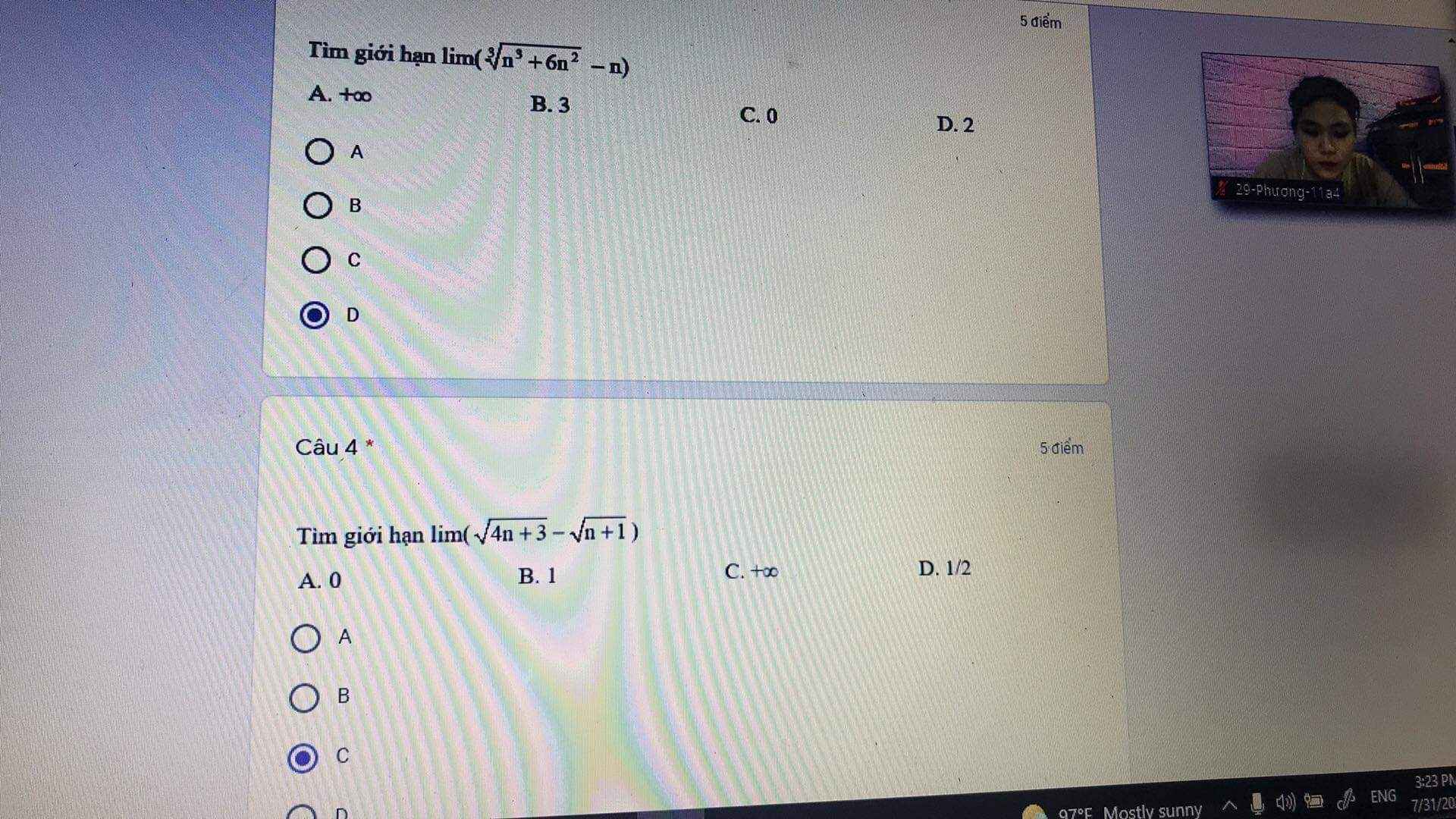
\(\lim\left(\sqrt{4n+3}-\sqrt{n-1}\right)=\lim\dfrac{3n+4}{\sqrt{4n+3}+\sqrt{n-1}}=\lim\dfrac{3+\dfrac{4}{n}}{\sqrt{\dfrac{4}{n}+\dfrac{3}{n^2}}+\sqrt{\dfrac{1}{n}-\dfrac{1}{n^2}}}=\dfrac{3}{0}=+\infty\)

\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{4x^2+x}+2x-1\right)\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{4x^2+x-\left(2x-1\right)^2}{\sqrt{4x^2+x}-2x+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{4x^2+x-4x^2+4x-1}{\sqrt{4x^2+x}-2x+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{5x-1}{-x\cdot\sqrt{4+\dfrac{1}{x}}-2x+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{5-\dfrac{1}{x}}{-\sqrt{4+\dfrac{1}{x}}-2+\dfrac{1}{x}}\)
\(=\dfrac{5-0}{-\sqrt{4+0}-2+0}=\dfrac{5}{-4}=-\dfrac{5}{4}\)

em vẽ hình sai nhưng làm đúng thì em vẫn như người làm sai vì em đã bị lạc đề nên em vẫn bị trừ điểm bài đó như chưa từng làm .

\(tanx=-tan\dfrac{\pi}{5}\)
\(\Leftrightarrow tanx=tan\left(-\dfrac{\pi}{5}\right)\)
\(\Leftrightarrow x=-\dfrac{\pi}{5}+k\pi\)
Mình quên mất, nó nằm trong khoảng (π/2; π) nha, mình xin lỗi

số số hạng là :
\(\left(2018-1\right):1+1=2018\)
tổng trên bằng
\(\left(\frac{1}{2018}+\frac{1}{2}\right).2018:2\)
\(=\frac{1010}{2018}.2018:2\)
\(=1010:2=505\)
P/s : ko chắc >: hình như sai
Công thức tính tổng
{(Số đầu + số cuối). số số hạng } :2

EG là đường trung bình tam giác MNP \(\Rightarrow\left\{{}\begin{matrix}EG||MN\\EG=\dfrac{1}{2}MN=x\end{matrix}\right.\)
FG là đường trung bình tam giác MPQ \(\Rightarrow\left\{{}\begin{matrix}FG=\dfrac{1}{2}PQ=x\sqrt{2}\\FG||PQ\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=\widehat{\left(EG;FG\right)}\)
\(cos\widehat{EGF}=\dfrac{EG^2+FG^2-EF^2}{2EG.FG}=-\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{EGF}=135^0\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=180^0-135^0=45^0\)
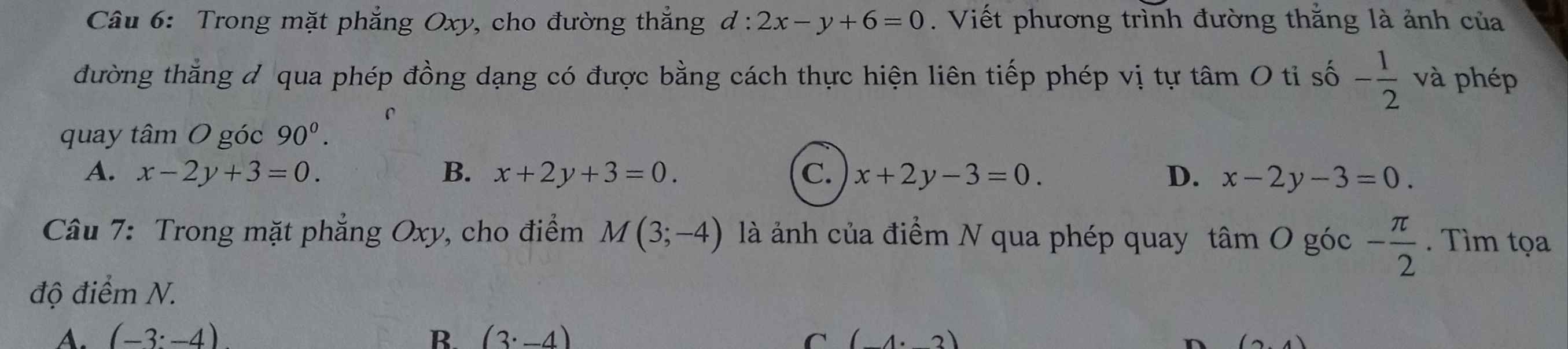

Chọn C