Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khối lượng niken trong 140 tấn vụn thép chứa 30% niken là: 140.30%= 42 (tấn)
Gọi khối lượng thép cần lấy loại chứa 10% niken là x (tấn) (0<x<140)
Gọi khối lượng thép cần lấy loại chứa 35% niken là y (tấn ) (0<y<140)
Vì tổng khối lượng thép cần lấy là 140 tấn, nên ta có ptrình (1):
(1) x+y= 140
Mặt khác, khối lượng niken cần lấy ta biểu diễn theo ptrình (2) là:
10%x+35%y= 42
<=> 0,1x +0,35y= 42 (2)
Từ các phương trình (1), (2) ta có hệ:
{x+y=1400,1x+0,35y=42{x+y=1400,1x+0,35y=42
Giaỉ hệ phương trình: x= 28 ; y=112 (nhận)
Vậy: Cần lấy 28 tấn thép vụn loại chứa 10% niken
Và lấy 112 tấn thép vụn loại chứa 35% niken
Khối lượng Niken trong 140 tấn thép vụn là: 140.30%=42 tấn
Gọi x (tấn) là khối lượng thỏi chứa 10% Niken; y là khối lượng thỏi 35% Niken (x, y >0)
Theo đề bài ta có phương trình:
{x+y=14010%x+35%y=42⇔{x=28y=112{x+y=14010%x+35%y=42⇔{x=28y=112

Câu 1:
Khối lượng đồng trong hợp kim ban đầu: \(12.45\%=5,4\left(kg\right)\)
Gọi khối lượng thiếc cần thêm vào là \(x\) (kg), ta có:
\(\frac{5,4}{12+x}=\frac{40}{100}=\frac{2}{5}\)
\(\Leftrightarrow2\left(12+x\right)=27\)
\(\Rightarrow x=1,5\left(kg\right)\)
Câu 2:
Gọi khối lượng nước cần thêm vào là \(x\left(g\right)\), ta có:
\(\frac{40}{x+150}=\frac{20}{100}=\frac{1}{5}\)
\(\Leftrightarrow x+150=200\)
\(\Rightarrow x=50\left(g\right)\)
Câu 3:
Số cá màu đỏ ban đầu trong hồ: \(200.99\%=198\) con
Gọi số cá đỏ cần bỏ đi là \(x\), ta có pt:
\(\frac{198-x}{200-x}=\frac{98}{100}=\frac{49}{50}\)
\(\Leftrightarrow50\left(198-x\right)=49\left(200-x\right)\)
\(\Rightarrow x=100\) (con)
Câu 4:
Gọi số thép vụn loại 10% là x, loại 35% là y (tấn)
Khối lượng Niken trong loại 1: \(x.10\%=\frac{x}{10}\) tấn
Khối lượng Niken trong loại 2: \(y.35\%=\frac{7y}{20}\)
Ta có hệ pt:
\(\left\{{}\begin{matrix}x+y=140\\\frac{\frac{x}{10}+\frac{7y}{20}}{140}=\frac{30}{100}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=140\\2x+7y=840\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=28\\y=112\end{matrix}\right.\)

Gọi khối lượng của 2 loại thép lần lượt và x và y (>0) tấn
Khối lượng Niken trong 2 loại thép lần lượt là \(0.05x\) và \(0.4y\) tấn
Theo bài ra ta có pt:
\(\left\{{}\begin{matrix}x+y=140\\\frac{0.05x+0.4y}{140}=0.3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=40\\y=100\end{matrix}\right.\)

Gọi khối lượng mỗi quặng là a và b (tấn)
ta có: \(\frac{70a+40b}{a+b}=60\Leftrightarrow\frac{30a}{a+b}+40=60\Leftrightarrow30a=20\left(a+b\right)\Leftrightarrow10a=20b\Leftrightarrow a=2b\)
lại có\(\frac{70\left(a-8\right)+40\left(b-2\right)}{\left(a-8\right)+\left(b-2\right)}=58\Leftrightarrow\frac{30\left(a-8\right)}{a-8+b-2}+40=58\Leftrightarrow30\left(a-8\right)=18\left(a+b-10\right)\)
\(\Leftrightarrow30a-240=18a+18b-180\Leftrightarrow12a-18b=60\)
thay a=2b vào phương trình trên ta có
\(12\times2b-18b=60\Leftrightarrow24b-18b=60\Leftrightarrow6b=60\Leftrightarrow b=10\Rightarrow a=20\)
Vậy khối lượng quặng 1 là 20 tấn, khối lượng quặng 2 là 10 tấn

Gọi khối lượng quặng loại thứ nhất là x ( tấn), loại thứ hai là y (tấn)
Điều kiện: x > 0; y > 0
Lượng sắt nguyên chất có trong mỗi loại quặng bằng lượng sắt có trong hỗn hợp ta có phương trình:
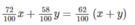
Thêm mỗi loại quặng 15 tấn ta được hỗn hợp chứa 63,25% sắt, ta có phương trình:
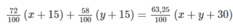
Ta có hệ phương trình:
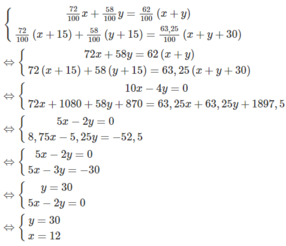
Cả hai giá trị x = 12; y = 30 thỏa mãn điều kiện bài toán.
Vậy loại quặng thứ nhất có 12 tấn, loại quặng thứ hai có 30 tấn.

Để cho ra quặng 66% thì cần trộn tỷ lệ quặng 75% : quặng 50% là 82/75 : 1 hay 82/75 : 75/75.
Như vậy để có 25 tấn quặng 66% thì cần:
Quặng 75%
(82 x 25) : (82 + 75)= 2075/157 tấn
Quặng 50%
(75 x25) :(82+75)= 1875/157 tấn

gọi x,y là số tấn quặng sắt loại I và loại II đã trộn với nhau lúc ban đầu
khi đó
phần trăm quặng sắt của hỗn hợp trên là \(\frac{0.7x+0.4y}{x+y}=0.6\)
phần trăm của quặng sắt của hỗn hợp sau là \(\frac{0.7\left(x+5\right)+0.4\left(y-5\right)}{x+5+y-5}=0.65\Leftrightarrow\frac{0.7x+0.4y+0.15}{x+y}=0.65\)
hay \(\frac{0.7x+0.4y}{x+y}+\frac{1.5}{x+y}=0.65\Rightarrow\frac{1.5}{x+y}=0.05\Rightarrow x+y=30\Rightarrow0.7x+0.4y=18\)
từ đây ta giải hệ \(\hept{\begin{cases}x+y=30\\0.7x+0.4y=18\end{cases}\Leftrightarrow\hept{\begin{cases}x=20\\y=10\end{cases}}}\)