Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Câu trả lời của alibaba nguyễn đúng mà hài!!!)
Sơ đồ Horner hoạt động như sau:
| 1 | 0 | a | b | c | |
| 3 | 1 | 3 | a+9 | 3a+b+27 | 9a+3b+c+27 |
| 3 | 1 | 6 | a+27 | 6a+b+108 | 27a+6b+c+351 |
| 3 | ... | ... | ... | ... | ... |
- Kẻ bảng, trên dòng đầu tiên ghi các hệ số của đa thức đầu tiên, ở đây là \(1,0,a,b,c\).
- Theo định lí Bezout thì đa thức sẽ có nghiệm bội 3 là số 3, do đó chừa một cột bên tay trái ghi nghiệm (là số 3).
- Hạ hệ số (là 1) xuống, thực hiện quy tắc "nhân ngang cộng chéo" (nhân từ nghiệm qua rồi cộng chéo lên).
- VD: 3 nhân 1 cộng 0 là 3, viết 3. 3 nhân 3 cộng a là a+9, viết a+9. 3 nhân (a+9) cộng b là 3a+b+27, viết 3a+b+27...
- Để 3 là nghiệm của đa thức thì hệ số cuối cùng là 0, tức là \(9a+3b+c+27=0\).
- Tự làm tiếp, ra thêm 2 cái phương trình nữa...

Cau a va b dat cot tim so du .Vi la phep chia het nen du bang 0.Cau c thi da thuc se chia het cho tich (x+3)(x-3) lam tuong tu hai cau a va b

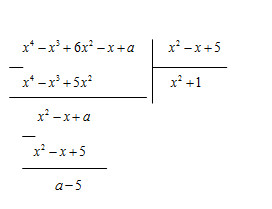
Vậy a = 5 thì đa thức x^4 - x^3 + 6x^2 - x +a chia hết cho đa thức x^2 - x + 5

\(f\left(x\right)=ax^3+bx+c\)
\(\hept{\begin{cases}f\left(-2\right)=0\\f\left(1\right)=1+5=6\\f\left(-1\right)=-1+5=4\end{cases}}\Leftrightarrow\hept{\begin{cases}-8a-2b+c=0\\a+b+c=6\\-a-b+c=4\end{cases}}\Leftrightarrow\hept{\begin{cases}a=b=\frac{1}{2}\\c=5\end{cases}}\)




F(-2)=0=> -8a+4b+c=0 (1)
f(1)=6=> a+b+c=6 (2)
f(-1)=4=> -a+b+c=4 (3)
(2) trừ (3)=> 2a=2=> a=1; thay vào (3)=> c=5-b thay vào (1)
-8+4b+5-b=0=> b=1
\(\left\{{}\begin{matrix}a=-1\\b=1\\c=4\\f\left(x\right)=-x^3+x^2+4\end{matrix}\right.\)
Vì P(x) \(⋮\) 5 với \(\forall\) x
=> P(0) \(⋮\) 5 mà P(0) = c => c \(⋮\)5
P(1) \(⋮\) 5 mà P(1) = a+b+c => a+b \(⋮\) 5 (1)
P(-1) \(⋮\) 5 mà P(-1) = a-b+c => a-b \(⋮\) 5 (2)
Từ (1) và (2) suy ra (a+b) + (a-b) \(⋮\) 5
=> 2a \(⋮\) 5 => a \(⋮\) 5
mà a+b \(⋮\) 5 => b \(⋮\) 5
Vậy..