Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là \(x\) và \(y\) \(\left( {x,y \in \mathbb{N}} \right)\).
+ Theo giả thiết, thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất nên \(0 \le x \le 200\)
và 240 chiếc mũ kiểu thứ hai nên ta có \(0 \le y \le 240\)
+ Nếu chỉ sản xuất toàn kiểu mũ thứ hai thì trong 1 giờ phân xưởng làm được 60 chiếc
=> Thời gian làm \(1\) chiếc mũ kiểu thứ hai là 1/60 (giờ)
=> Thời gian làm \(y\) chiếc kiểu hai là \(\frac{y}{{60}}\left( h \right)\)
+ Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai
=> thời gian làm 1 chiếc mũ kiểu thứ nhất là 2.1/60 = 1/30 (giờ)
=> Thời gian làm \(x\) chiếc kiểu thứ nhất là \(\frac{x}{{30}}\left( h \right)\)
+ Tổng thời gian làm một ngày không quá 8h nên ta có:
\(\frac{x}{{30}} + \frac{y}{{60}} \le 8\)
Bước 2: Lập hệ bất phương trình.
\(\left\{ \begin{array}{l}
0 \le x \le 200\\
0 \le y \le 240\\
\frac{x}{{30}} + \frac{y}{{60}} \le 8
\end{array} \right.\)
Bước 3: Biểu diễn miền nghiệm.
Miền biểu diễn miền nghiệm là phần không bị gạch, đa giác OABCD với O(0;0), A(0; 240), B(120; 240), C(200; 80), D(200; 0).
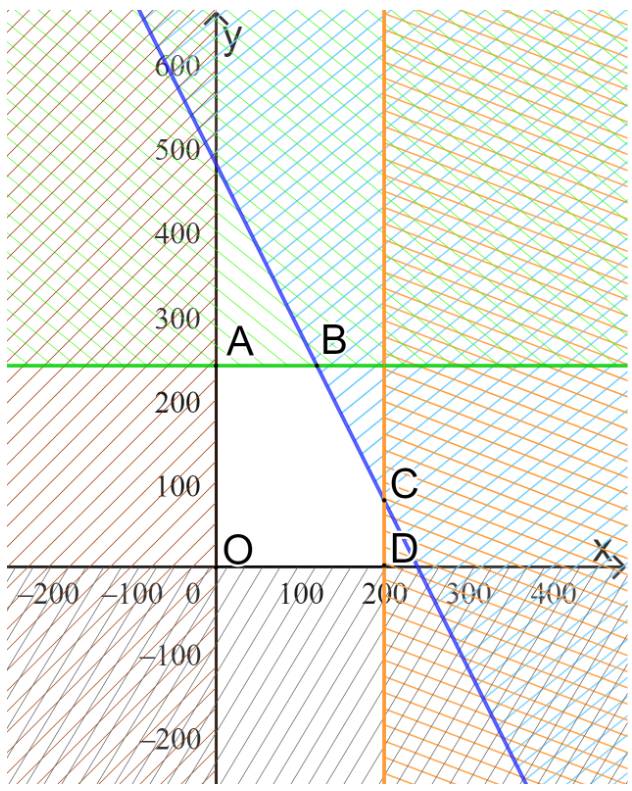
Bước 4: Tìm \(x\) và \(y\) để tiền lãi cao nhất.
Từ miền nghiệm ta thấy tiền lãi cao nhất tại khi điểm \(\left( {x;y} \right)\) là một trong các đỉnh của đa giác OABCD.
\(T = 24x + 15y\)
\(T\left( {0;240} \right) = 15.240 = 3600\) (nghìn đồng)
\(T\left( {120;240} \right) = 24.120+15.240 = 6480\) (nghìn đồng)
\(T\left( {200;80} \right) = 24.200+15.80 = 6000\) (nghìn đồng)
\(T\left( {200;0} \right) = 24.200 = 4800\)(nghìn đồng)
Vậy để tiền lãi thu được nhiều nhất, mỗi ngày xưởng cần sản xuất số mũ kiểu 1 là 120 và mũ kiểu 2 là 240 cái.

a: \(2^{10}:2^8=2^2=4\)
b: \(4^6:4^3=4^3=64\)
c: \(8^5:8^4=8^{5-4}=8\)
c: \(7^4:7^4=7^0=1\)

1: \(\dfrac{16^{11}\cdot5^{40}}{10^{41}}=\dfrac{2^{44}\cdot5^{40}}{2^{41}\cdot5^{41}}=\dfrac{2^3}{5^1}=\dfrac{8}{5}\)
2: \(\dfrac{3^7\cdot8^5}{6^6\cdot\left(-2\right)^{12}}=\dfrac{3^7\cdot2^{15}}{2^6\cdot3^6\cdot2^{12}}=\dfrac{3}{2^3}=\dfrac{3}{8}\)

a: \(=2^6\cdot2^{20}=2^{26}\)
b: \(=3^9\cdot3^8\cdot3^2\cdot2\cdot13=3^{19}\cdot2\cdot13\)

a) \(\left(6x-5y\right)^2=36x^2-60xy+25y^2\)
b) \(\left(4x-1\right)^2=16x^2-8x+1\)
c) \(\left(x+2\right)^2=x^2+4x+4\)
d) \(x^2-64=\left(x-8\right)\left(x+8\right)\)
e) \(4x^2-64=\left(2x-8\right)\left(2x+8\right)\)
f) \(25x^2-4=\left(5x-2\right)\left(5x+2\right)\)
g) \(\left(x+1\right)^3=x^3+3x^2+3x+1\)
h) \(\left(x-3\right)^3=x^3-9x^2+27x-27\)
k) \(x^3+8=\left(x+2\right)\left(x^2-2x+4\right)\)
l) \(x^3-125=\left(x-5\right)\left(x^2+5x+25\right)\)
y) \(27y^3-1=\left(3y-1\right)\left(9y^2+3y+1\right)\)

a: \(7\cdot3^x=5\cdot3^7+2\cdot3^7\)
\(\Leftrightarrow7\cdot3^x=7\cdot3^7\)
=>3x=37
hay x=7
b: \(4^{x+3}-3\cdot4^{x+1}=13\cdot4^{11}\)
\(\Leftrightarrow4^{x+1}\left(4^2-3\right)=13\cdot4^{11}\)
=>x+1=11
hay x=10
d: \(\left(x-1\right)^{13}=\left(x-1\right)^{12}\)
\(\Leftrightarrow\left(x-1\right)^{12}\left(x-2\right)=0\)
hay \(x\in\left\{1;2\right\}\)

\(A=1+2+2^2+.....+2^{2018}\)
\(\Leftrightarrow2A=2+2^2+....+2^{2018}+2^{2019}\)
\(\Leftrightarrow2A-A=\left(2+2^2+....+2^{2019}\right)-\left(1+2+2^2+....+2^{2018}\right)\)
\(\Leftrightarrow A=2^{2019}-1< 2^{2019}\)
Vậy \(A< 2^{2019}\)
a, 2^3=8, 2^4=16,2^5=32, 2^6=64, 2^7=128, 2^8=256, 2^9=512, 2^10=1024
b, 3^2=9, 3^3=27, 3^4=81, 3^5=243
c, 4^2=16, 4^3=64, 4^4=256
d, 5^2=25, 5^3=125, 5^4=625
e, 6^2=36, 6^3=216, 6^4= 1296