HA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 10 2017
a/ \(2^x=32\)
\(\Leftrightarrow2^x=2^5\)
\(\Leftrightarrow x=5\)
Vậy...
b/ \(\left(x+3\right)^2=81\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=9\\x+3=-9\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=6\\x=-12\end{matrix}\right.\)
Vậy ....
c/ \(3^{x+3}=243\)
\(\Leftrightarrow3^{x+3}=3^5\)
\(\Leftrightarrow x+3=5\)
\(\Leftrightarrow x=2\)
Vậy ....
d/ \(\left(2x-5\right)^3=64\)
sai đề thì p
NP
2
KV
21 tháng 10 2020
*) So sánh 354 và 281
Ta có:
354 = (32)27 = 927
281 = (23)27 = 827
Do 9 > 8 \(\Rightarrow\) 927 > 827
Vậy 354 > 281
*) So sánh 536 và 1124
Ta có:
536 = (53)12 = 12512
1124 = (112)12 = 12112
Do 125 > 121 nên 12512 > 12112
Vậy 536 > 1124
*) So sánh 7.213 và 216
Ta có:
216 = 23.213 = 8.213
Do 7 < 8 nên 7.213 < 8.213
Vậy 7.213 < 216
DK
1
7 tháng 12 2022
1000 chia hết cho 4
nên 2^2000 có chữ số tận cùng là 6
161 là số lẻ
nên 4^161 có chữ số tận cùng là 6
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Gọi \(\bar a\) là đường kính thực của nhân tế bào.
Vì phép đo đường kính nhân tế bào cho kết quả là \(5 \pm 0,3\mu m\).
=> \(a = 5\mu m;d = 0,3\mu m\)
Nên ta có \(\bar a\) nằm trong đoạn \(\left[ {5 - 0,3;5 + 0,3} \right]\) hay \(\left[ {4,7;5,3} \right]\).
TQ
1
5 tháng 1 2021
Ta có: \(\left\{{}\begin{matrix}\overrightarrow{a}=m\overrightarrow{u}+\overrightarrow{v}=\left(4m+1;m+4\right)\\\overrightarrow{b}=\overrightarrow{i}+\overrightarrow{j}=\left(1;1\right)\end{matrix}\right.\)
Yêu cầu bài toán <=> cos\(\left(\overrightarrow{a};\overrightarrow{b}\right)\)=cos45o =\(\dfrac{\sqrt{2}}{2}\)
<=> \(\dfrac{\left(4m+1\right)+\left(m+4\right)}{\sqrt{2}\sqrt{\left(4m+1\right)^2+\left(m+4\right)^2}}=\dfrac{\sqrt{2}}{2}\)
<=> \(\dfrac{5\left(m+1\right)}{\sqrt{2}\sqrt{17m^2+16+17}}=\dfrac{\sqrt{2}}{2}\)
<=> \(5\left(m+1\right)=\sqrt{17m^2+16m+17}\) <=>\(\left\{{}\begin{matrix}m+1\ge0\\25m^2+50m+25=17m^2+16m+17\end{matrix}\right.\)
<=> m=\(-\dfrac{1}{4}\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
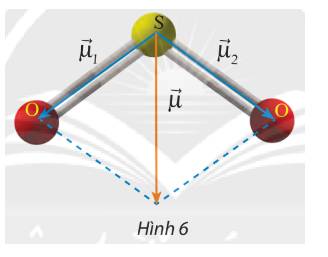
Từ điểm cuối của vectơ \(\overrightarrow {{\mu _1}} \) vẽ vectơ \(\overrightarrow {{\mu _3}} = \overrightarrow {{\mu _2}} \)
Suy ra \(\overrightarrow \mu = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _2}} = \overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} \Rightarrow \left| {\overrightarrow \mu } \right| = \left| {\overrightarrow {{\mu _1}} + \overrightarrow {{\mu _3}} } \right|\)
Ta có: \(\left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _2}} } \right) = 120^\circ \Rightarrow \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right) = 60^\circ \)
\( \Rightarrow {\left| {\overrightarrow \mu } \right|^2} = {\left| {\overrightarrow {{\mu _1}} } \right|^2} + {\left| {\overrightarrow {{\mu _3}} } \right|^2} - 2\left| {\overrightarrow {{\mu _1}} } \right|\left| {\overrightarrow {{\mu _3}} } \right|\cos \left( {\overrightarrow {{\mu _1}} ,\overrightarrow {{\mu _3}} } \right)\)
\( = 1,{6^2} + 1,{6^2} - 2.1,6.1,6.\cos 60^\circ = \frac{{64}}{{25}}\)
\( \Rightarrow \left| {\overrightarrow \mu } \right| = \sqrt {\frac{{64}}{{25}}} = 1,6\)
Vậy độ dài của \(\overrightarrow \mu \) là 1,6 đơn vị
\(=\dfrac{\left(-5\right)^5\cdot2^4}{5^4\cdot2^4}=\left(-5\right)\)