K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0

N
3

1 tháng 2 2021
Có : \(P=4x+\dfrac{16}{x^2}=2x+2x+\dfrac{16}{x^2}\)
- AD AMGM : \(2x+2x+\dfrac{16}{x^2}\ge3\sqrt[3]{\dfrac{2x.2x.16}{x^2}}=12\)
- Dấu " = " xảy ra \(\Leftrightarrow2x=\dfrac{16}{x^2}\)
\(\Leftrightarrow2x^3=16\)
\(\Leftrightarrow x=2\) ( TM )
Vậy ....
( Chắc đề như vầy :vvv )
NP
5


CM
5 tháng 3 2019
Đáp án: A
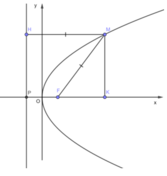
(P): y 2 = x ⇒ p = 1/2
Ta có:
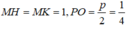
Hoành độ của điểm M chính là độ dài đoạn OK
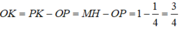
bấm máy tính là ra thôi
ko bao giờ ra đâu bạn