K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1
7 tháng 7 2022
b: \(=\dfrac{-5}{7}\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+\dfrac{13}{4}=\dfrac{-5}{7}+\dfrac{13}{4}=\dfrac{-20+91}{28}=\dfrac{71}{28}\)
c: \(=\dfrac{146}{13}-3-\dfrac{68}{13}=6-3=3\)
d: \(=\dfrac{2}{7}\left(\dfrac{21}{4}-\dfrac{13}{4}\right)=\dfrac{4}{7}\)
17 tháng 7 2022
1: \(=75\left(27+25-2\right)=75\cdot50=3750\)
2: \(=15\left(23+37\right)+55=15\cdot60+55=955\)
3: \(=36\cdot14+36\cdot17+36\cdot69\)
\(=36\cdot100=3600\)
4: \(=200\cdot\left(32+68\right)=200\cdot100=20000\)
PT
1
CM
15 tháng 2 2019
Ta thấy:
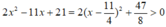
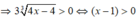
Áp dụng bất đẳng thức Cô – si ta có:
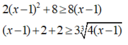
Cộng vế với vế ta được:
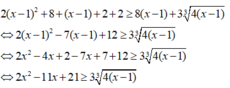
Dấu “=” xảy ra khi và chỉ khi x - 1 = 2 ⇔ x = 3
Vậy x = 3 là nghiệm của phương trình.
TT
23 tháng 11 2017
a,\(\left|9+x\right|=2x\)
\(\Leftrightarrow\left[{}\begin{matrix}9+x=2x\\9x+x=-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}9=x\\9=-3x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-3\end{matrix}\right.\)
Vậy...
Trường hợp 2 chưa chắc chắn lắm!!!
NN
23 tháng 11 2017
a) \(\left|9+x\right|=2x\)
Xét trường hợp 1:
\(9+x=2x\)
\(\Leftrightarrow9+x-2x=0\)
\(\Leftrightarrow9-x=0\)
\(\Leftrightarrow x=9\)
Xét trường hợp 2:
\(9+x=-2x\)
\(\Leftrightarrow9+x-\left(-2x\right)=0\)
\(\Leftrightarrow9+x+2x=0\)
\(\Leftrightarrow9+3x=0\)
\(\Leftrightarrow3x=-9\)
\(\Leftrightarrow x=-9:3\)
\(\Leftrightarrow x=-3\)
Vậy x=9 hoặc x=-3
b) \(\left|x+6\right|-9=2x\)
\(\Leftrightarrow\left|x+6\right|=2x+9\)
Xét trường hợp 1:
\(x+6=2x+9\)
\(\Leftrightarrow x+6-\left(2x+9\right)=0\)
\(\Leftrightarrow x+6-2x-9=0\)
\(\Leftrightarrow-3-x=0\)
\(\Leftrightarrow x=-3\)
Xét trường hợp 2:
\(x+6=-\left(2x+9\right)\)
\(\Leftrightarrow x+6-\left[-\left(2x+9\right)\right]=0\)
\(\Leftrightarrow x+6+\left(2x+9\right)=0\)
\(\Leftrightarrow x+6+2x+9=0\)
\(\Leftrightarrow3x+15=0\)
\(\Leftrightarrow3x=-15\)
\(\Leftrightarrow x=-15:3\)
\(\Leftrightarrow x=-5\)
Vậy x=-3 hoặc x=-5
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2020
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge16\\y\ge9\end{matrix}\right.\)
Từ pt thứ nhất của hệ:
\(\frac{8xy}{x^2+y^2+6xy}+\frac{17}{8}\left(\frac{x}{y}+\frac{y}{x}\right)=\frac{21}{4}\)
\(\Leftrightarrow\frac{8}{\frac{x}{y}+\frac{y}{x}+6}+\frac{17}{8}\left(\frac{x}{y}+\frac{y}{x}\right)=\frac{21}{4}\)
Đặt \(\frac{x}{y}+\frac{y}{x}=t\ge2\)
\(\Rightarrow\frac{8}{6+t}+\frac{17}{8}t=\frac{21}{4}\)
\(\Leftrightarrow\frac{17}{8}t^2+\frac{15}{2}t-\frac{47}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2\\t=-\frac{94}{17}< 0\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\frac{x}{y}+\frac{y}{x}=2\Leftrightarrow x^2+y^2=2xy\)
\(\Leftrightarrow\left(x-y\right)^2=0\Leftrightarrow x=y\)
Thay xuống pt dưới:
\(\sqrt{x-16}+\sqrt{x-9}=7\)
\(\Leftrightarrow\sqrt{x-16}-3+\sqrt{x-9}-4=0\)
\(\Leftrightarrow\frac{x-25}{\sqrt{x-16}+3}+\frac{x-25}{\sqrt{x-9}+4}=0\)
\(\Leftrightarrow...\)
VM
1
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2021
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge-\dfrac{9}{2}\\x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{\left(3+\sqrt{9+2x}\right)^2.2x^2}{\left(3-\sqrt{9+2x}\right)^2\left(3+\sqrt{9+2x}\right)^2}< x+21\)
\(\Leftrightarrow\dfrac{\left(3+\sqrt{9+2x}\right)^2.2x^2}{4x^2}< x+21\)
\(\Leftrightarrow\left(3+\sqrt{9+2x}\right)^2< 2x+42\)
\(\Leftrightarrow x+9+3\sqrt{9+2x}< x+21\)
\(\Leftrightarrow\sqrt{9+2x}< 4\)
\(\Leftrightarrow9+2x< 16\Rightarrow x< \dfrac{7}{2}\)
Vậy \(\left\{{}\begin{matrix}-\dfrac{9}{2}\le x< \dfrac{7}{2}\\x\ne0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 2 2020
Chắc dưới mẫu bạn ghi nhầm căn đầu tiên
ĐKXĐ: \(-21\le x\le21;x\ne0\)
\(\Leftrightarrow\frac{\left(\sqrt{21+x}+\sqrt{21-x}\right)^2}{21+x-21+x}=\frac{21}{x}\)
\(\Leftrightarrow\frac{42+2\sqrt{21^2-x^2}}{2x}=\frac{21}{x}\)
\(\Leftrightarrow\sqrt{21^2-x^2}=0\)
\(\Rightarrow x=\pm21\)
\(43+\left(9-21\right)=317-\left(x+317\right)\)
\(43+9-21=317-x-317\)
\(31=317-317-x\)
\(31=0-x\)
\(\Rightarrow x+0=-31\)
\(x=\left(-31\right)-0\)
\(x=-31\)
\(43+\left(9-21\right)=317-\left(x+317\right)\)
\(43+\left(-12\right)=317+x-317\)
\(31=317+x+\left(-317\right)\)
\(31=317+\left(-317\right)+x\)
\(31=0+x\)
\(31=x\)
\(\Leftrightarrow x=31\)
Vậy \(x=31\) là giá trị cần tìm