Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn kiểm tra lại đề. Và vào hoc 24 để đăng nhé!
Làm câu cuối:
TXĐ: \(x\in\)[ 0 ; + vô cùng )
\(y'=\frac{1}{2\sqrt{x}}-1=0\Leftrightarrow2\sqrt{x}=1\Leftrightarrow x=\frac{1}{4}\left(tm\right)\)
Vẽ bảng biến thiên:
....
Từ bảng biên thiên:
Hàm số đồng biến trong khoảng ( 0 ; 1/4 )
Hàm số nghịch biên trong khoảng ( 1/4 ; + dương vô cùng)

a) Tập xác định : D = R { 1 }.
> 0, ∀x
1.
Hàm số đồng biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
b) Tập xác định : D = R { 1 }.
< 0, ∀x
1.
Hàm số nghịch biến trên các khoảng : (-∞ ; 1), (1 ; +∞).
c) Tập xác định : D = (-∞ ; -4] ∪ [5 ; +∞).
∀x ∈ (-∞ ; -4] ∪ [5 ; +∞).
Với x ∈ (-∞ ; -4) thì y’ < 0; với x ∈ (5 ; +∞) thì y’ > 0. Vậy hàm số nghịch biến trên khoảng (-∞ ; -4) và đồng biến trên khoảng (5 ; +∞).
d) Tập xác định : D = R { -3 ; 3 }.
< 0, ∀x
±3.
Hàm số nghịch biến trên các khoảng : (-∞ ; -3), (-3 ; 3), (3 ; +∞).

a) y′=6x2+6x−36=6(x2+x−6)y′=6x2+6x−36=6(x2+x−6)
y’= 0 ⇔ x2+ x – 6= 0 ⇔ x=2; x=-3
Bảng biến thiên :
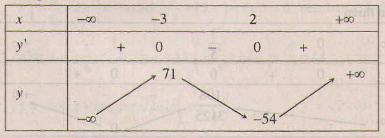
Hàm số đạt cực đại tại x = -3 , ycđ = y(-3) = 71
Hàm số đạt cực tiểu tại x = 2 , y(ct) = y(2) = -54
b) y’ = 4x3 + 4x = 4x(x2 + 1); y’ = 0 ⇔ x = 0.
Bảng biến thiên :
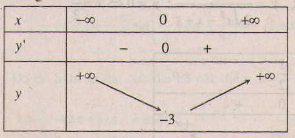
Hàm số đạt cực tiểu tại x = 0 , y(ct) = y(0) = -3
c) Tập xác định : D = R\{0}

Bảng biến thiên :
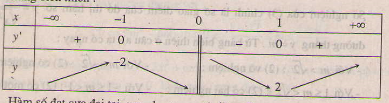
Hàm số đạt cực đại tại x = -1 , ycđ = y(-1) = -2 ;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 2.
d) Tập xác định : D = R.
y’ = 3x2(1 – x)2 + x3 . 2(1 – x)(-1) = x2 (1 – x)[3(1 – x) - 2x] = x2 (x – 1)(5x – 3) .
y’ = 0 ⇔ x = 0, x = , x = 1.
, x = 1.
Bảng biến thiên :
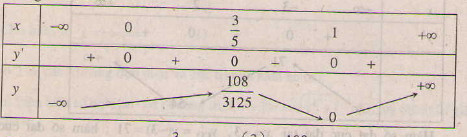
Hàm số đạt cực đại tại x =  , ycđ =
, ycđ =  =
=  ;
;
Hàm số đạt cực tiểu tại x = 1 , yct = y(1) = 0 .
e) Tập xác định : D = R. 
Hàm số đạt cực tiểu tại 

Lời giải:
Ta có:
\(A=\int \frac{x\sin x+\cos x}{x^2-\cos ^2x}dx=\int \frac{(\cos x-x)+x(\sin x+1)}{x^2-\cos ^2x}dx\)
\(=-\int \frac{dx}{\cos x+x}+\int \frac{x(\sin x+1)}{x^2-\cos ^2x}dx=-\int \frac{dx}{x+\cos x}+\frac{1}{2}\int (\sin x+1)\left(\frac{1}{x-\cos x}+\frac{1}{x+\cos x}\right)dx\)
\(=-\int \frac{dx}{x+\cos x}+\frac{1}{2}\int (\sin x+1)\frac{dx}{x-\cos x}+\frac{1}{2}\int (\sin x-1)\frac{dx}{x+\cos x}+\int \frac{dx}{x+\cos x}\)
\(=\frac{1}{2}\int (\sin x+1)\frac{dx}{x-\cos x}+\frac{1}{2}\int (\sin x-1)\frac{dx}{x+\cos x}\)
\(=\frac{1}{2}\int \frac{d(x-\cos x)}{x-\cos x}+\frac{1}{2}\int \frac{-d(x+\cos x)}{x+\cos x}\)
\(=\frac{1}{2}\ln |x-\cos x|-\frac{1}{2}\ln |x+\cos x|+c\)
Xét biểu thức $B$
\(B=\int \frac{\ln x-1}{x^2-\ln ^2x}dx=\int \frac{(\ln x-x)+(x-1)}{x^2-\ln ^2x}dx\)
\(=-\int \frac{dx}{x+\ln x}+\int \frac{x-1}{x^2-\ln ^2x}dx=-\int \frac{dx}{x+\ln x}+\frac{1}{2}\int \frac{(x-1)}{x}\left(\frac{1}{x-\ln x}+\frac{1}{x+\ln x}\right)dx\)
\(=-\int \frac{dx}{x+\ln x}+\frac{1}{2}\int \frac{1}{x-\ln x}.\frac{x-1}{x}dx+\frac{1}{2}\int \frac{1}{x+\ln x}.\frac{x-1}{x}dx\)
\(=-\int \frac{dx}{x+\ln x}+\frac{1}{2}\int \frac{1}{x-\ln x}.\frac{x-1}{x}dx-\frac{1}{2}\int \frac{1}{x+\ln x}.\frac{1+x}{x}dx+\int \frac{dx}{x+\ln x}\)
\(=\frac{1}{2}\int \frac{1}{x-\ln x}.\frac{x-1}{x}dx-\frac{1}{2}\int \frac{1}{x+\ln x}.\frac{1+x}{x}dx\)
\(=\frac{1}{2}\int \frac{d(x-\ln x)}{x-\ln x}-\frac{1}{2}\int \frac{d(x+\ln x)}{x+\ln x}\)
\(=\frac{1}{2}\ln |x-\ln x|-\frac{1}{2}\ln |x+\ln x|+c\)

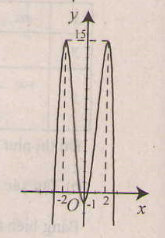
a) Tập xác định : R ; y' =-4x3 + 16x = -4x(x2 - 4);
y' = 0 ⇔ x = 0, x = ±2 .
Bảng biến thiên :
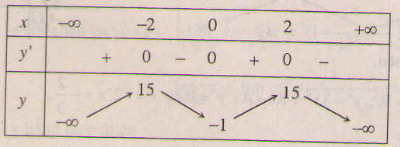
Đồ thị như hình bên.
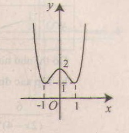
b) Tập xác định : R ; y' =4x3 - 4x = 4x(x2 - 1);
y' = 0 ⇔ x = 0, x = ±1 .
Bảng biến thiên :
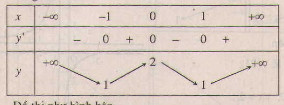
Đồ thị như hình bên.
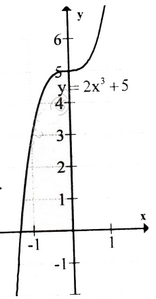
c) Tập xác định : R ; y' =2x3 + 2x = 2x(x2 + 1); y' = 0 ⇔ x = 0.
Bảng biến thiên :
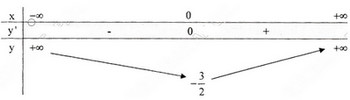
Đồ thị như hình bên.
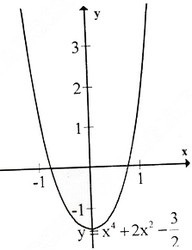
d) Tập xác định : R ; y' = -4x - 4x3 = -4x(1 + x2); y' = 0 ⇔ x = 0.
Bảng biến thiên :
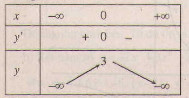
Đồ thị như hình bên.
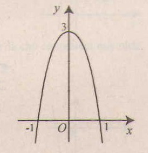 .
.

a) Tập xác định: R; y' = 3(1 - x2); y' = 0 ⇔ x = ± 1 .
Bảng biến thiên :
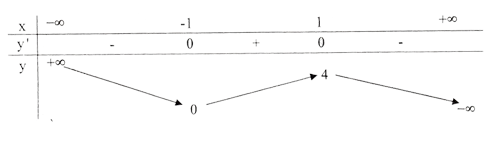
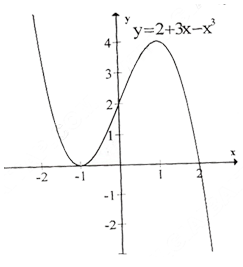
Đồ thị như hình bên.
b) Tập xác định : R ; y' = 3x2 + 8x + 4; y' = 0 ⇔ x= -2, x = ![]() .
.
Bảng biến thiên :
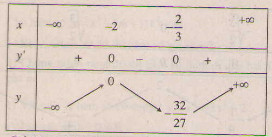
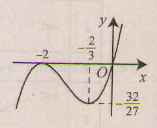
Đồ thị như hình bên.
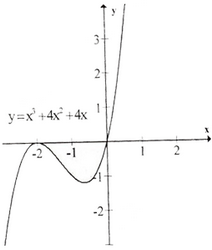
c) Tập xác định : R ;
y' = 3x2 + 2x + 9 > 0, ∀x. Vậy hàm số luôn đồng biến, không có cực trị.
Bảng biến thiên :
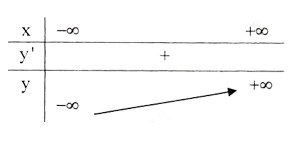
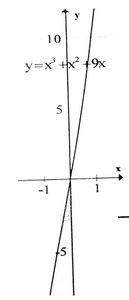
Đồ thị hàm số như hình bên.
d) Tập xác định : R ;
y' = -6x2 ≤ 0, ∀x. Vậy hàm số luôn nghịch biến, không có cực trị.
Bảng biến thiên :
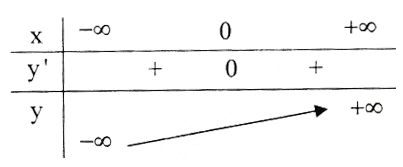
Đồ thị hàm số như hình bên.
Lời giải hay đó!!!
Nhưng không biết người giải nó có hiểu nó không....![]() (thở dài)
(thở dài)

a) Vì ![]() và
và ![]() ( hoặc
( hoặc ![]() và
và ![]() ) nên các đường thẳng: x = -3 và x = 3 là các tiệm cận đứng của đồ thị hàm số.
) nên các đường thẳng: x = -3 và x = 3 là các tiệm cận đứng của đồ thị hàm số.
Vì ![]() và
và ![]() nên các đường thẳng: y = 0 là các tiệm cận ngang của đồ thị hàm số.
nên các đường thẳng: y = 0 là các tiệm cận ngang của đồ thị hàm số.
b) Hai tiệm cận đứng : ![]() ; tiệm cận ngang :
; tiệm cận ngang : ![]() .
.
c) Tiệm cận đứng : x = -1 ;
vì ![]() nên đồ thị hàm số không có tiệm cận ngang.
nên đồ thị hàm số không có tiệm cận ngang.
d) Hàm số xác định khi : ![]()
Vì ![]() ( hoặc
( hoặc ![]() ) nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
) nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Vì .png) nên đường thẳng y = 1 là tiệm cận ngang (về bên phải) của đồ thị hàm số.
nên đường thẳng y = 1 là tiệm cận ngang (về bên phải) của đồ thị hàm số.

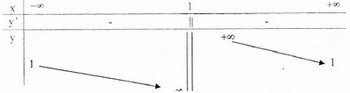
a) Tập xác định : R\ {1}; y′=−4(x−1)2<0,∀x≠1y′=−4(x−1)2<0,∀x≠1 ;
Tiệm cận đứng : x = 1 . Tiệm cận ngang : y = 1.
Bảng biến thiên :
Đồ thị như hình bên. 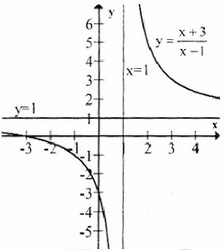
b) Tập xác định : R \{2}; y′=6(2x−4)2>0,∀x≠2y′=6(2x−4)2>0,∀x≠2
Tiệm cận đứng : x = 2 . Tiệm cận ngang : y = -1.
Bảng biến thiên :
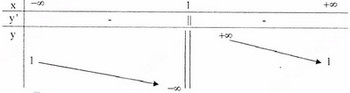
Đồ thị như hình bên.
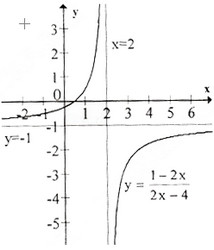
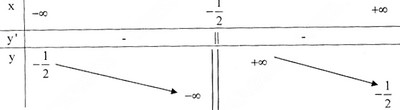
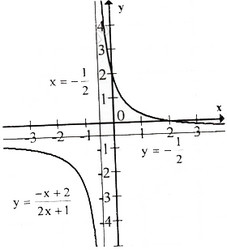
c) Tập xác định : R∖{−12}R∖{−12}; y′=−5(2x+1)2<0,∀x≠−12y′=−5(2x+1)2<0,∀x≠−12
Tiệm cận đứng : x=−12x=−12 . Tiệm cận ngang : y=−12y=−12.
Bảng biến thiên :
Đồ thị như hình bên.

`a)TXĐ:R\\{1;1/3}`
`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`
`b)TXĐ:R`
`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`
`c)TXĐ: (4;+oo)`
`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`
`d)TXĐ:(0;+oo)`
`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`
`e)TXĐ:(-oo;-1)uu(1;+oo)`
`y'=-7x^[-8]-[2x]/[x^2-1]`
Lời giải:
a.
$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$
$=-4(3x^2-4x+1)^{-5}(6x-4)$
$=-8(3x-2)(3x^2-4x+1)^{-5}$
b.
$y'=(3^{x^2-1})'+(e^{-x+1})'$
$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$
$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$
c.
$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$
$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$
d.
\(y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2\)
\(=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}\)
e.
\(y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}\)