Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì \(\widehat{mOp}\) đối đỉnh với \(\widehat{nOq}\) mà 2 góc đối đỉnh thì bằng nhau ,\(\widehat{mOp}\)=60độ \(\Rightarrow\) \(\widehat{nOq}\)= 60 độ
Vì tia Op và tia Oq đối nhau \(\Rightarrow\) \(\widehat{mOp}+\widehat{mOq}\)= 180 độ ( vì 2 góc đó kề bù )
\(\Rightarrow\)\(\widehat{mOq}\)= 180 độ - \(\widehat{mOp}\)
Hay : \(\widehat{mOq}\)=180 độ - 60 độ
Vậy :\(\widehat{mOq}\)= 120 độ
b, vì ot là tpg của góc mOp mà mOt = tOp = 1/2 x 60 = 30 độ mà góc nOq là góc đối đỉnh của mOp mà tia ot lại là tia đối của ot' \(\Rightarrow\)góc nOt' = t'Oq (=30 độ) và ot' nằm giữa vì ot nằm giữa om và op mà ot lại là tia đối ot' .
Vậy ot' là tpg của góc nOq
c, Các góc đối đỉnh là góc nhọn : góc nOp và mOq , góc tOm và nOt' ,góc tOp và t'Oq , góc mOpvaf nOq
đấy giải rồi đấy k đúng đê

#)Giải :
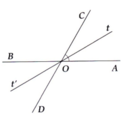
A B C D O t t'
a) Vì góc AOC và góc BOD là hai góc đối đỉnh => góc AOC = góc BOD ( = 60o)
Vì góc AOC và góc BOC là hai góc kề bù => góc BOC = 180o - góc AOC = 180o - 60o = 120o
Vì góc BOC và góc AOD là hai góc đối đỉnh => góc BOC = góc AOD ( = 120o)
b) Vì Ot là tia phân giác của góc AOC => góc AOt = góc COt = 60o/2 = 30o
Vì góc AOt và góc BOt' là hai góc đối đỉnh => góc AOt = góc BOt' ( = 30o)
Vì góc COt và góc DOt' là hai góc đối đỉnh => góc COt = góc DOt' ( = 30o)
=> góc BOt' = góc DOt' ( = 30o)
=> Ot' là tia phân giác của góc BOD
C B D A o t t'
Giải
a) +) Vì \(\widehat{AOC}\)và \(\widehat{BOD}\) là 2 góc đối đỉnh
=> \(\widehat{AOC}\) = \(\widehat{BOD}\) = 60o
+) Vì \(\widehat{COB}\) và \(\widehat{BOD}\)là 2 góc kề bù
=> \(\widehat{COB}\)+ \(\widehat{BOD}\)= 180o
Hay \(\widehat{COB}\)+ 60o = 180o
\(\widehat{COB}\) = 180o - 60o = 120o
+) Vì \(\widehat{COB}\)và \(\widehat{AOD}\)là 2 góc đối đỉnh
=> \(\widehat{COB}\)= \(\widehat{AOD}\) = 120o
b) Vì Ot là tia phân giác của \(\widehat{AOC}\)
=> \(\widehat{AOt}\)= \(\widehat{tOC}\)= \(\frac{\text{}\widehat{AOC}}{2}\)= \(\frac{60^o}{2}\)= 30o
Vì \(\widehat{AOt}\)và \(\widehat{BOt'}\)là 2 góc đối đỉnh
=> \(\widehat{AOt}\)= \(\widehat{BOt'}\)= 30o
Vì \(\widehat{COt}\)và \(\widehat{DOt'}\)là 2 góc đối đỉnh
=> \(\widehat{COt}\)= \(\widehat{DOt'}\)= 30o
=> \(\widehat{BOt'}\)= \(\widehat{DOt'}\)( = 30o ) ( 1 )
Trên cùng 1 nửa mặt phẳng bờ chứa tia OD có \(\widehat{DOt'}< \widehat{DOB}\)( vì 30o < 60o )
=> Ot' nằm giữa OB và OD ( 2 )
Từ ( 1 ) và ( 2 ) => Ot' là tia phân giác của \(\widehat{BOD}\)

a, MOP + NOP = 180 độ ( kề bù)
=> NOP =1 80 - NOP= 180 - 60 dộ = 120 dộ
Vì MOP và NOQ là hai góc đối đỉnh => MOP = NOQ = 60 độ
Vì NOP và MOQ là hai góc đối đỉnh => NOP = MOQ = 120 độ
b,OT là p/g MOP => POT = MOT = 1/2 POM = 1/2.60 độ = 30 độ
Vì POT và QOT' là hai góc đối đỉnh => POT = QOT" = 30 độ (1)
Vì MOT và NOT' là ..................... => MOT = NOT' = 30 độ (2)
Từ (1) và (2) => NOT' = QOT' = 30 độ => OT' là tia p/g NOQ
c, Các cặp góc đối đỉnh là góc nhọn :
(+) POT và QOT'
(+) MOT và NOT'
(+) POM và NOQ

a) B O D ^ = A O C ^ = 60° (đối đỉnh.).
=> C O B ^ + A O C ^ = 180° (kề bù), => B O C ^ = 180 ° − A O C ^ = 120°
=> A O D ^ = B O C ^ = 120° (đối đỉnh),
b) Vì Ot là phân giác góc AOC nên
A O t ^ = 1 2 A O C ^ = 30°
=> B O t ' ^ = A O t ^ = 30° (đối đỉnh).
Tương tự:
D O t ' ^ = 30 ° ⇒ B O t ' ^ = D O t ' ^
Do đó Ot' là phân giác của B O D ^ .