Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn


2: \(-4x^2+5x-2\)
\(=-4\left(x^2-\dfrac{5}{4}x+\dfrac{1}{2}\right)\)
\(=-4\left(x^2-2\cdot x\cdot\dfrac{5}{8}+\dfrac{25}{64}+\dfrac{7}{64}\right)\)
\(=-4\left(x-\dfrac{5}{8}\right)^2-\dfrac{7}{16}< =-\dfrac{7}{16}< 0\forall x\)
Sửa đề:\(f\left(x\right)=\dfrac{-x^2+4\left(m+1\right)x+1-4m^2}{-4x^2+5x-2}\)
Để f(x)>0 với mọi x thì \(\dfrac{-x^2+4\left(m+1\right)x+1-4m^2}{-4x^2+5x-2}>0\forall x\)
=>\(-x^2+4\left(m+1\right)x+1-4m^2< 0\forall x\)(1)
\(\text{Δ}=\left[\left(4m+4\right)\right]^2-4\cdot\left(-1\right)\left(1-4m^2\right)\)
\(=16m^2+32m+16+4\left(1-4m^2\right)\)
\(=32m+20\)
Để BĐT(1) luôn đúng với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< 0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}32m+20< 0\\-1< 0\left(đúng\right)\end{matrix}\right.\)
=>32m+20<0
=>32m<-20
=>\(m< -\dfrac{5}{8}\)

1. Ta có : 3x+12=0 <=> x= -4
bảng xét dấu:
| x | -∞ -4 + ∞ |
| 3x+12 |
- 0 + |
f(x) >0 ∀ x ∈ (-4;+∞)
f(x) <0 ∀ x∈ (-∞;-4)
2. Ta có : -5x+9=0 <=> x= \(\frac{9}{5}\)
Bảng xét dấu:
| x | -∞ 9/5 +∞ |
| -5x+9 | + 0 - |
f(x) >0 ∀ x ∈ (-∞; 9/5)
f(x) <0 ∀ x ∈(9/5; +∞)
3. Ta có : -3x-9=0 <=> x= -3
| x | -∞ -3 +∞ |
| -3x-9 | + 0 - |
f(x) >0 ∀ x∈ (-∞; -3)
f(x) <0 ∀x∈ ( -3; +∞ )
4. Ta có : x (2x+4)=0
+, x=0
+, 2x+4=0 <=> x= -2
| x | -∞ -2 0 +∞ |
| x | - \(|\) - 0 + |
| 2x+4 | - 0 + \(|\) + |
| f (x) | + 0 - 0 + |
f(x) >0 ∀ x ∈ (-∞; -2) \(\cup\) (0; +∞)
f(x) <0 ∀ x ∈ (-2;0)
5. Ta có: (x-2)(-x+4)=0
+, x-2=0 <=> x=2
+, -x+4=0 <=> x= 4
| x | -∞ 2 4 +∞ |
| x-2 | - 0 + \(|\) + |
| -x+4 | + \(|\) + 0 - |
| f(x) | - 0 + 0 - |
f(x) >0 ∀ x ∈ (2;4)
f (x) <0 ∀x∈ (-∞;2) \(\cup\)(4; +∞)
6. Ta có : (-4x+3)(x-6)=0
+, -4x+3=0 <=>x= \(\frac{3}{4}\)
+, x-6 =0 <=> x=6
| x | -∞ 3/4 6 +∞ |
| -4x+3 | + 0 - \(|\) - |
| x-6 | - \(|\) - 0 + |
| f(x) | - 0 + 0 - |
f(x) >0 ∀ x∈ (3/4;6)
f(x) <0 ∀ x∈ (-∞; 3/4) \(\cup\)(6;+∞)

Chọn A
Tam thức : -4x2+ 5x-1 có a= -4 và ∆ = -7< 0
suy ra -4x2+ 5x-1<0 với mọi x
Do đó h(x) luôn dương khi và chỉ khi
f(x) = -x2+ 4( m+1) x+ 1- 4m2 luôn âm
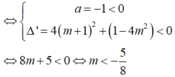
Vậy với m< -5/8 thì biểu thức h(x) luôn dương.

Chọn A.
Tam thức -4 x 2 + 5x - 2 có a = -4 <0, Δ = -7 < 0 suy ra -4 x 2 + 5x - 2 < 0, ∀x
Do đó 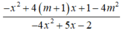
luôn dương khi và chỉ khi - x 2 + 4(m + 1)x + 1 - 4 m 2 luôn âm
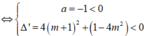

Vậy với 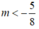 thì biểu thức
thì biểu thức 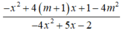 luôn dương.
luôn dương.