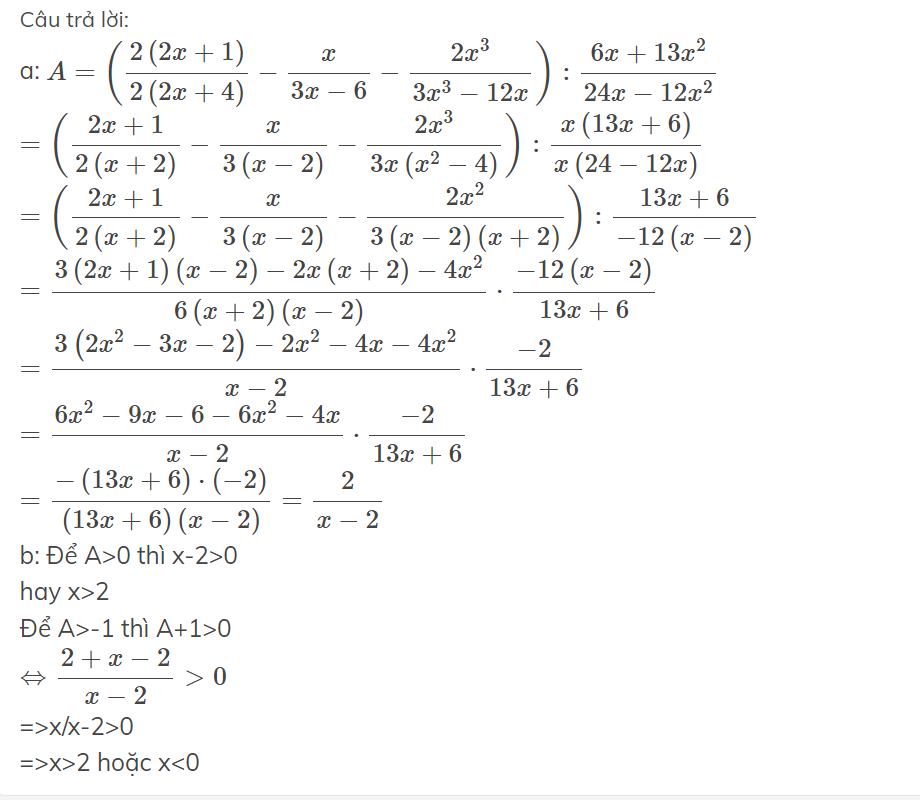VC
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VC
3
19 tháng 3 2020
(3x-2)(2x-1)=(2-3x)(x+3)
(3x-2)(2x-1)-(2-3x)(x+3)=0
(3x-2)(2x-1)+(3x-2)(x+3)=0
(3x-2)(2x-1+x+3)=0
(3x-2)(3x+2)=0
\(\orbr{\begin{cases}3x-2=0\\3x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}3x=2\\3x=-2\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{2}{3}\\x=\frac{-2}{3}\end{cases}}}\)
Vậy........
19 tháng 3 2020
(=) 6x2 - 3x - 4x - 2 = 2x + 6 - 3x2 -9x
(=) 6x2 +3x2 - 7x + 7x + 2 -6 = 0
(=) 9x2 - 4 = 0
(=) 9x2 = 4
(=) x2 = \(\frac{9}{4}\)
(=) x = +- \(\frac{3}{2}\)
VC
0
PA
25 tháng 1 2017
2x3 + 3x2 + 6x + 5 = 02
<=> 2x3 + x2 + 5x + 2x2 + x + 5 = 0
<=> x(2x2 + x + 5) + (2x2 + x + 5) = 0
<=> (2x2 + x + 5)(x + 1) = 0
<=> x + 1 = 0 (vì 2x2 + x + 5 \(\ge\) 4,875 > 0 \(\forall\) x)
<=> x = - 1
Vậy tập nghiệm của pt là \(S=\left\{-1\right\}\)
25 tháng 1 2017
b) 4x4 + 12x3 + 5x2 - 6x - 15 = 0
<=> 4x4 + 10x3 + 2x3 + 5x2 - 6x - 15 = 0
<=> 2x3(2x + 5) + x2(2x + 5) - 3(2x + 5) = 0
<=> (2x + 5)(2x3 + x2 - 3) = 0
<=> (2x + 5)(2x3 - 2x2 + 3x2 - 3) = 0
<=> (2x + 5)(x - 1)(2x2 + 3x + 3) = 0
<=> (2x + 5)(x - 1)[x2 + (x + 3/2)2 + 3/4]= 0
Mà x2 + (x + 3/2)2 + 3/4 > 0\(\forall x\)
\(\Rightarrow\left[\begin{matrix}2x+5=0\\x-1=0\end{matrix}\right.\)\(\Leftrightarrow\left[\begin{matrix}x=-\frac{5}{2}\\x=1\end{matrix}\right.\)
Vậy ...
22 tháng 3 2020
B A C N M
a, xét tam giác ABC có CN là pg của ^ACB (gt)
=> BN/NA = BC/AC (Đl) (1)
xét tam giác ABC có AM là pg của ^BAC (gt)
=> BM/CM = AB/AC (đl) (2)
có BC = AB (gt) (3)
(1)(2)(3) => BN/NA = BM/CM
=> MN // AC (đl)
TU
3
24 tháng 10 2016
\(x+2\sqrt{2x^2}+2x^3=0\)
\(\Leftrightarrow x+2x\sqrt{2}+2x^3=0\)
\(\Leftrightarrow x\left(1+2\sqrt{2}+2x^2\right)=0\)
\(\Leftrightarrow x=0\) ( Vì \(1+2\sqrt{2}+2x^2>0\) )
25 tháng 10 2016
Tìm x biết :
\(x+2\sqrt{2}x^2+2x^3=0\)
\(x\left(1+2\sqrt{2}x+2x^2\right)=0\)
\(x\left(1+\sqrt{2}x\right)^2=0\)
TH1 : x=0
TH2 : \(\left(1+\sqrt{2}x\right)^2=0\)
\(1+\sqrt{2}x=0\)
\(x=\frac{-1}{\sqrt{2}}\)
VM
15 tháng 2 2017
Đặt: \(a=x^2+3x+2\).
Khi đó phương trình đã cho trở thành: \(a\left(a+1\right)-2=0\)
\(\Leftrightarrow a^2+a-2=0\)
\(\Leftrightarrow\left(a-1\right)\left(a+2\right)=0\)
\(\Leftrightarrow\left[\begin{matrix}a=1\\a=-2\end{matrix}\right.\)
Với a=1 thì \(x^2+3x+2=1\)
\(\Leftrightarrow\left(x^2+2.\frac{3}{2}x+\frac{9}{4}\right)-\frac{5}{4}=0\)
\(\Leftrightarrow\left(x+\frac{3}{2}\right)^2-\left(\frac{\sqrt{5}}{2}\right)^2=0\)
\(\Leftrightarrow\left[\begin{matrix}x=\frac{-3+\sqrt{5}}{2}\\x=\frac{-3-\sqrt{5}}{2}\end{matrix}\right.\)
Với a=-2 thì \(x^2+3x+2=-2\)
\(\Leftrightarrow\left(x^2+2.\frac{3}{2}x+\frac{9}{4}\right)+\frac{7}{4}=0\)
\(\Leftrightarrow\left(x+\frac{3}{2}\right)^2+\frac{7}{4}=0\) (Phương trình vô nghiệm)
Vậy: phương trình trên có tập nghiệm là S={\(\frac{-3+\sqrt{5}}{2};\frac{-3-\sqrt{5}}{2}\)}