
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Dat sin x = y
y2 - 3y - 4= 0
y = -1 hoac y = 4 (loai)
voi y = -1 thi sin x = -1 => \(x=-\frac{\pi}{2}+2k\pi\)
b) Chia hai ve cho 2 ta co:
\(\frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx=sin2x\)
\(cos\frac{\pi}{6}sinx+sin\frac{\pi}{6}cosx=sin2x\)
\(sin\left(x+\frac{\pi}{6}\right)=sin2x\)
\(x+\frac{\pi}{6}=2x+2k\pi\) hoac \(x+\frac{\pi}{6}=\pi-2x+2k\pi\)

a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)

4.
\(\Leftrightarrow2sinx.cosx-\left(1-2sin^2x\right)+3sinx-cosx-1=0\)
\(\Leftrightarrow cosx\left(2sinx-1\right)+2sin^2x+3sinx-2=0\)
\(\Leftrightarrow cosx\left(2sinx-1\right)+\left(2sinx-1\right)\left(sinx+2\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+cosx+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2sinx-1=0\\sinx+cosx=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\sin\left(x+\frac{\pi}{4}\right)=-\sqrt{2}< -1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)
2.
ĐKXĐ: ...
\(\Leftrightarrow cot\left(\frac{\pi}{4}-x\right)=-\frac{1}{\sqrt{3}}\)
\(\Leftrightarrow\frac{\pi}{4}-x=-\frac{\pi}{3}+k\pi\)
\(\Leftrightarrow x=\frac{7\pi}{12}+k\pi\)
3.
\(\Leftrightarrow cos\frac{x}{4}sinx+sin\frac{x}{4}.cosx-3\left(sin^2x+cos^2x\right)+cosx=0\)
\(\Leftrightarrow sin\left(x+\frac{x}{4}\right)=-cosx\)
\(\Leftrightarrow sin\frac{5x}{4}=sin\left(x-\frac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\frac{5x}{4}=x-\frac{\pi}{2}+k2\pi\\\frac{5x}{4}=\frac{3\pi}{2}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)

Lời giải:
Đặt $\sin x=a; \cos x=b(a,b\in [-1;1])$ thì ta có:
\(\left\{\begin{matrix} 3a+b+2=0\\ a^2+b^2=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=-(3a+2)\\ a^2+b^2=1\end{matrix}\right.\)
\(\Rightarrow a^2+(3a+2)^2=1\)
\(\Leftrightarrow 10a^2+12a+3=0\Rightarrow a=\frac{-6\pm \sqrt{6}}{10}\)
Với $a=\frac{-6\pm \sqrt{6}}{10}$ thì \(x=2k\pi +\arcsin \frac{-6+\sqrt{6}}{10}\) hoặc \(x=(2k+1)\pi -\arcsin \frac{-6+\sqrt{6}}{10}\)Với $a=\frac{-6-\sqrt{6}}{10}$ thì \(x=2k\pi +\arcsin \frac{-6-\sqrt{6}}{10}\) hoặc \(x=(2k+1)\pi -\arcsin \frac{-6-\sqrt{6}}{10}\)
Với $k$ nguyên nào đó.
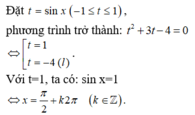
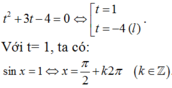
Hự, toán lp 11 lận
Trả lơi
Bạn có thể qua hh.vn nha
Nếu ko ai trả lời
Chúc bạn học tốt !