
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a)|x|-9=-2+17
|x|-9 = 15
|x| = 15 + 9
|x| = 24
\(\Rightarrow x=\mp24\)
b)|x-9|=-2+17
|x-9| = 15
\(\Rightarrow\orbr{\begin{cases}x-9=15\\x-9=-15\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=24\\x=-6\end{cases}}\)
Hok tốt !
a)|x|-9=-2+17
| x| -9 = 15
| x | = 15 + 9
| x| = 24
Vậy x= 24 hoặc x = -24
b)|x-9|=-2+17
| x -9| = 15
Th1: x - 9 = 15
x = 15 + 9
x = 24
Th2 : x - 9 = -15
x = -15 + 9
x = -6
vậy x = 24 hoặcx = -6
hok tốt!!!

1/ 12 . 194 + 6 . 437 . 2 + 3 . 369 . 4
= 12 . 194 + 12 . 437 + 12 . 369
= 12(194 + 437 + 369)
= 12 . 1000
= 12000
2/ 1 + 5 + 9 + 19 + ... + 61 + 65 . 2 - 26
= (1 + 61) + (5 + 57) + ... + (29 + 33) + 130 - 26
= 62 . 8 + 130 - 26
= (496 - 26) + 130
= 470 + 130
= 600
3/ (1374 x 57 + 687 x 86) : (26 x 13 + 74 x 14)
= (1374 x 57 + 1374 x 43) : (26 x 13 + 74 x 13 + 74)
= (1374 x 100) : (13 x 100 + 74)
= 137400 : 1374 = 100

\(=\frac{3}{4}+\frac{11}{10}:\left(\frac{2}{5}-\frac{3}{2}\right)-\frac{1}{9}\)
\(=\frac{3}{4}+\frac{11}{10}:-\frac{11}{10}-\frac{1}{9}\)
\(=\frac{3}{4}+-1-\frac{1}{9}\)
\(=-\frac{1}{4}-\frac{1}{9}\)
\(=-\frac{13}{36}\)
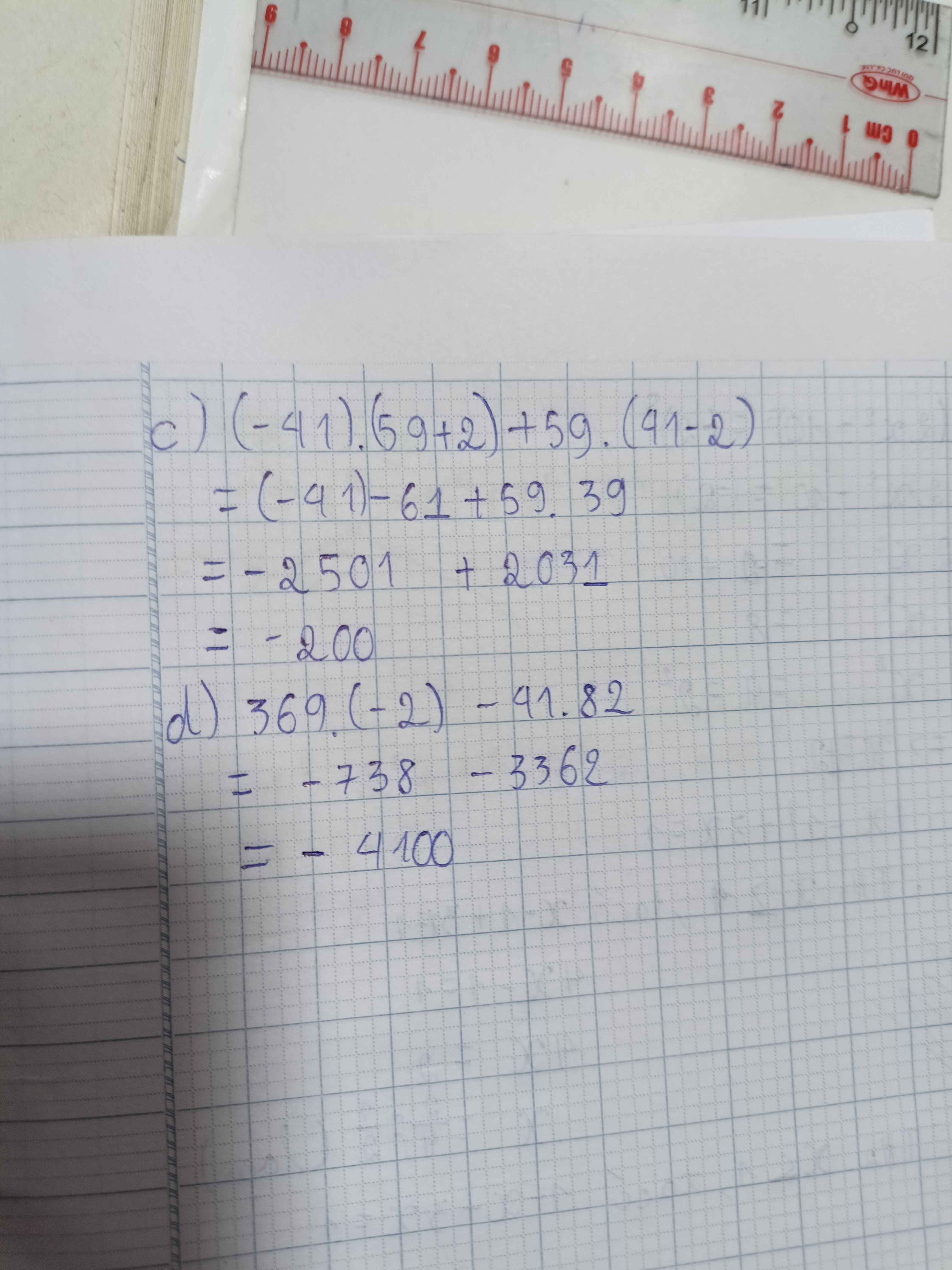
Tui dùng máy tính,ra -4100
= -738 - 1148
= -1886