K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H9
HT.Phong (9A5)
CTVHS
4 tháng 10 2023
\(\sqrt{32}+\sqrt{50}-2\sqrt{8}+\dfrac{1}{3}\sqrt{18}\)
\(=\sqrt{4^2\cdot2}+\sqrt{5^2\cdot2}-2\cdot2\sqrt{2}+\dfrac{1}{3}\cdot\sqrt{3^2\cdot2}\)
\(=4\sqrt{2}+5\sqrt{2}-4\sqrt{2}+\dfrac{1}{3}\cdot3\sqrt{2}\)
\(=\left(4\sqrt{2}-4\sqrt{2}\right)+5\sqrt{2}+\sqrt{2}\)
\(=5\sqrt{2}+\sqrt{2}\)
\(=6\sqrt{2}\)
CM
15 tháng 7 2019
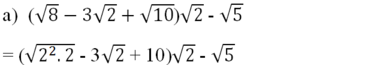
= (2√2 - 3√2 + 10)√2 - √5
= 2.(√2)2 - 3.(√2)2 + √10.√2 - √5
= 4 - 6 + √20 - √5 = -2 + 2√5 - √5
= -2 + √5
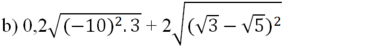
= 0,2.10.√3 + 2|√3 - √5|
s
= 2√3 + 2(√5 - √3)
= 2√3 + 2√5 - 2√3 = 2√5
30 tháng 7 2021
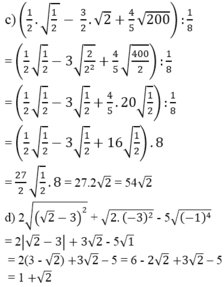
a) Ta có: \(A=\sqrt{20}-10\sqrt{\dfrac{1}{5}}+\sqrt{\left(\sqrt{5}-1\right)^2}\)
\(=2\sqrt{5}-2\sqrt{5}+\sqrt{5}-1\)
\(=\sqrt{5}-1\)
b) Ta có: \(B=2\sqrt{32}+5\sqrt{8}-4\sqrt{32}\)
\(=8\sqrt{2}+10\sqrt{2}-16\sqrt{2}\)
\(=2\sqrt{2}\)
15 tháng 12 2022
\(=5\sqrt{2}-\dfrac{3}{2}\cdot4\sqrt{2}-\dfrac{1}{3}\cdot6\sqrt{2}+8=-3\sqrt{2}+8\)
AH
Akai Haruma
Giáo viên
29 tháng 7 2021
Cần gấp thì bạn cũng nên viết đầy đủ đề bài nhé.
** Bài toán rút gọn**
Lời giải:
\(\sqrt{17-12\sqrt{2}}=\sqrt{17-2\sqrt{72}}=\sqrt{9-2\sqrt{8.9}+8}=\sqrt{(\sqrt{9}-\sqrt{8})^2}\)
\(=\sqrt{9}-\sqrt{8}=3-2\sqrt{2}\)
\(\sqrt{24-8\sqrt{8}}=\sqrt{24-2\sqrt{128}}=\sqrt{16-2\sqrt{16.8}+8}=\sqrt{(\sqrt{16}-\sqrt{8})^2}\)
\(=\sqrt{16}-\sqrt{8}=4-2\sqrt{2}\)
\(\Rightarrow \sqrt{17-12\sqrt{2}}-\sqrt{24-8\sqrt{8}}=(3-2\sqrt{2})-(4-2\sqrt{2})=-1\)
--------------------
\(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}=\sqrt{17-12\sqrt{2}}+\sqrt{17+12\sqrt{2}}\)
\(=\sqrt{8-2\sqrt{8.9}+9}+\sqrt{8+2\sqrt{8.9}+9}\)
\(=\sqrt{(\sqrt{8}-\sqrt{9})^2}+\sqrt{(\sqrt{8}+\sqrt{9})^2}\)
\(=|\sqrt{8}-\sqrt{9}|+|\sqrt{8}+\sqrt{9}|=3-2\sqrt{2}+3+2\sqrt{2}=6\)
----------------------
\(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}=\sqrt{9+2\sqrt{9.2}+2}-\sqrt{9-2\sqrt{9.2}+2}\)
\(=\sqrt{(\sqrt{9}+\sqrt{2})^2}-\sqrt{(\sqrt{9}-\sqrt{2})^2}\)
\(=|\sqrt{9}+\sqrt{2}|-|\sqrt{9}-\sqrt{2}|=3+\sqrt{2}-(3-\sqrt{2})=2\sqrt{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
\(\sqrt{17-12\sqrt{2}}-\sqrt{24-8\sqrt{8}}=\sqrt{\left(3-2\sqrt{2}\right)^2}-\sqrt{\left(4-2\sqrt{2}\right)^2}\)
\(=\left|3-2\sqrt{2}\right|-\left|4-2\sqrt{2}\right|=3-2\sqrt{2}-4+2\sqrt{2}\)
\(=-1\)
\(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}=\sqrt{\left(3-2\sqrt{2}\right)^2}+\sqrt{\left(3+2\sqrt{2}\right)^2}\)
\(=\left|3-2\sqrt{2}\right|+\left|3+2\sqrt{2}\right|=3-2\sqrt{2}+3+2\sqrt{2}\)
\(=6\)
\(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}=\sqrt{\left(3+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=\left|3+\sqrt{2}\right|-\left|3-\sqrt{2}\right|=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)
CX
2
21 tháng 9 2017
lấy số cuối trừ số đầu chia khoảng cách cộng 1
Ta Tách từng số ra VD:1 và 2 khoảng cách là 1.Cứ như thế rồi suy ra
30 tháng 10 2023
a: \(\dfrac{\sqrt{50}-\sqrt{32}+\sqrt{8}}{\sqrt{2}}\)
\(=\dfrac{5\sqrt{2}-4\sqrt{2}+2\sqrt{2}}{\sqrt{2}}\)
\(=\dfrac{3\sqrt{2}}{\sqrt{2}}=3\)
b: \(\dfrac{4}{\sqrt{5}-1}-5\sqrt{\dfrac{1}{5}}\)
\(=\dfrac{4\left(\sqrt{5}+1\right)}{5-1}-\sqrt{5}\)
\(=\sqrt{5}+1-\sqrt{5}\)
=1
19 tháng 11 2016
\(A=8\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)+11\)
\(=\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)+11\)
\(=\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)+11\)
\(=\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)+11\)
\(=\left(3^{16}-1\right)\left(3^{16}+1\right)\left(3^{32}+1\right)+11\)
\(=\left(3^{32}-1\right)\left(3^{32}+1\right)+11\)
\(=\left(3^{64}-1\right)+11=3^{64}+10\)
19 tháng 11 2016
A = 8.(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1) + 1
A = (32 - 1)(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1) + 1
A = (34 - 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1) + 1
A = (38 - 1)(38 + 1)(316 + 1)(332 + 1) + 1
A = (316 - 1)(316 + 1)(332 + 1) + 1
A = (332 - 1)(332 + 1) + 1
A = 364 - 1 + 1
A = 364
đề nghị bạn tô ku đa,lol ko ns bậy trên trang học tập
Trả lời:
\(\sqrt{32}-\sqrt{8}+\sqrt{\frac{1}{2}}\)
\(=\sqrt{4^2.2}-\sqrt{2^2.2}+\sqrt{\frac{2}{2^2}}\)
\(=4\sqrt{2}-2\sqrt{2}+\frac{\sqrt{2}}{2}\)
\(=\left(4-2+\frac{1}{2}\right)\sqrt{2}\)
\(=\frac{5\sqrt{2}}{2}\)