Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
3. Cho ABC có I,K lần lượt là trung điểm của AB,AC. Trên tia IK lấy E sao cho IK=KE. Nối E với C
a. Chứng minh: AKI= CKE
BC
ta có BD=ED(gt)
\(\Rightarrow\frac{2}{3}BD=\frac{2}{3}ED\Rightarrow BI=ED\left(1\right)\)
\(BD=ED\Rightarrow\frac{1}{3}BD=\frac{1}{3}ED\Rightarrow ID=DK\)
lại có:\(DE=\frac{1}{3}DE+\frac{1}{3}DE+\frac{1}{3}DE\)
\(\Rightarrow\frac{2}{3}DE=DK+ID\left(DK=ID\right)\)
\(\Rightarrow KE=IK\left(2\right)\)
từ \(\left(1\right)\left(2\right)\Rightarrow BI=IK=KE\)
a)xét tam giác AKI và tam giác CKM có
KI =KM (giả thiết )
góc AKI = góc CKM ( 2 góc đối đỉ̉nh )
AK= CK ( K là trung điểm của CA )
suy ra tam giác AHI = tam giác CKM
b) tam giác AKI= tam giác CKM
suy ra góc MCK =góc KAI ( 2 GÓC TƯƠNG ƯỚNG)
mà chúng ở vị trí so le trong do AC cắt AI và MC
suy ra AI // MC
c ) MK 0 BIEI LAM
a) Xét ΔAKI và ΔCKM , ta có :
AK = KC ( k là trung điểm của AC )
IK = KM ( gt )
Góc AKI = MKC ( 2 góc đối đỉnh )
=> ΔAKI = ΔCKM (cgc )
b) Ta có : ΔAKI = ΔCKM
=> KMC = KIA ( 2 góc tương ứng )
mà góc KMC và KIA là hai góc ở vị trí so le trong
=> AI // MC
c)Ta có :
+ MC = AI ( ΔAKI = ΔCKM )
+ AI = IB ( I là trung điểm của AB )
=> MC = IB
+ MI // AI => MI // IB
Xét ΔMCI và ΔCIB , có :
MC = IB ( c/m t )
IC là cạnh chung
Góc MCI = CIB ( 2 góc so le trong , MC // IB )
=> ΔMCI = ΔBIC ( cgc )
=> Góc MIC = BCI ( 2 góc tương ứng )
mà MIC và BCI là góc góc ở vị trí so le trong
=> IK // BC
Ta có : IK = \(\frac{MI}{2}\) => IK = \(\frac{1}{2}MI\)
Mà BC = MI ( ΔMCI = ΔBIC )
=> IK = \(\frac{BC}{2}\Rightarrow IK=\frac{1}{2}BC\)
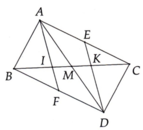
b: Xét tứ giác AICE có
K là trung điểm của AC
K là trung điểm của IE
Do đó: AICE là hình bình hành
Suy ra: AI//CE