NT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
L
2
19 tháng 3 2020
a) ( Y + 1 ) X + Y + 1 = 10
<=> ( Y + 1 ) X + ( Y + 1 ) =10
<=> ( Y + 1 ) ( X + 1 ) = 10
X; Y thuộc Z nên X+1 ; Y +1 thuộc Z và \(\inƯ\left(10\right)\in\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
Ta có bảng sau :
| X+1 | -1 | -2 | -5 | -10 | 1 | 2 | 5 | 10 |
| Y+1 | -10 | -5 | -2 | -1 | 10 | 5 | 2 | 1 |
| X | -2 | -3 | -6 | -11 | 0 | 1 | 4 | 9 |
| Y | -11 | -6 | -3 | -2 | 9 | 4 | 1 | 0 |
Vậy (X:Y) \(\in\){(-2;-11);(-3;-6);(-6;-3);(-11;-2);(0;9);(9;0);(1;4);(4;1)}
19 tháng 3 2020
b) ( 2X +1)Y - 2X - 1 = -31
<=> ( 2X + 1)(Y-1) = -31
Vì X;Y \(\in\)Z
=> 2X+1 ; Y+1 \(\in\)Z
=> 2X+1 ; Y+1 \(\in\)Ư(-32)
Vì 2X là số chẵn với mọi X \(\in\)Z => 2X +1 là số lẻ với mọi X\(\in\)Z
Ta có bảng :
| 2X+1 | -1 | 1 |
| Y-1 | 32 | -32 |
| X | -1 | 0 |
| Y | 33 | -31 |
Vậy ( X;Y ) \(\in\){ (-1;33);(0;-31)}
10 tháng 9 2021
Bài 2:
a: Ta có: \(2^{x+1}\cdot3^y=12^x\)
\(\Leftrightarrow2^{x+1}\cdot3^y=2^{2x}\cdot3^x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=2x\\x=y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
NV
0
MV
8 tháng 8 2017
\(\dfrac{2x}{15}+\dfrac{2x}{35}+\dfrac{2x}{63}+...+\dfrac{2x}{195}=\dfrac{4}{5}\\ x\cdot\left(\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+...+\dfrac{2}{195}\right)=\dfrac{4}{5}\\ x\cdot\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{13\cdot15}\right)=\dfrac{4}{5}\\ x\cdot\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{13}-\dfrac{1}{15}\right)=\dfrac{4}{5}\\ x\cdot\left(\dfrac{1}{3}-\dfrac{1}{15}\right)=\dfrac{4}{5}\\ x\cdot\dfrac{4}{15}=\dfrac{4}{5}\\ x=\dfrac{4}{5}:\dfrac{4}{15}\\ x=3\)
Gọi \(D=\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{32}-\dfrac{1}{64}\)
\(2D=1-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{16}-\dfrac{1}{32}\\ 2D+D=\left(1-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{16}-\dfrac{1}{32}\right)+\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{32}-\dfrac{1}{64}\right)\\ 3D=1-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{16}-\dfrac{1}{32}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{32}-\dfrac{1}{64}\\ 3D=1-\dfrac{1}{64}< 1\\ \Rightarrow D=\dfrac{1-\dfrac{1}{64}}{3}< \dfrac{1}{3}\)
Vậy \(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{32}-\dfrac{1}{64}< \dfrac{1}{3}\)
10 tháng 4 2022
Câu 1:
a: =>-2x-x+17=34+x-25
=>-3x+17=x+9
=>-4x=-8
hay x=2
b: =>17x+16x+27=2x+43
=>33x+27=2x+43
=>31x=16
hay x=16/31
c: =>-2x-3x+51=34+2x-50
=>-5x+51=2x-16
=>-7x=-67
hay x=67/7
e: 3x-32>-5x+1
=>8x>33
hay x>33/8
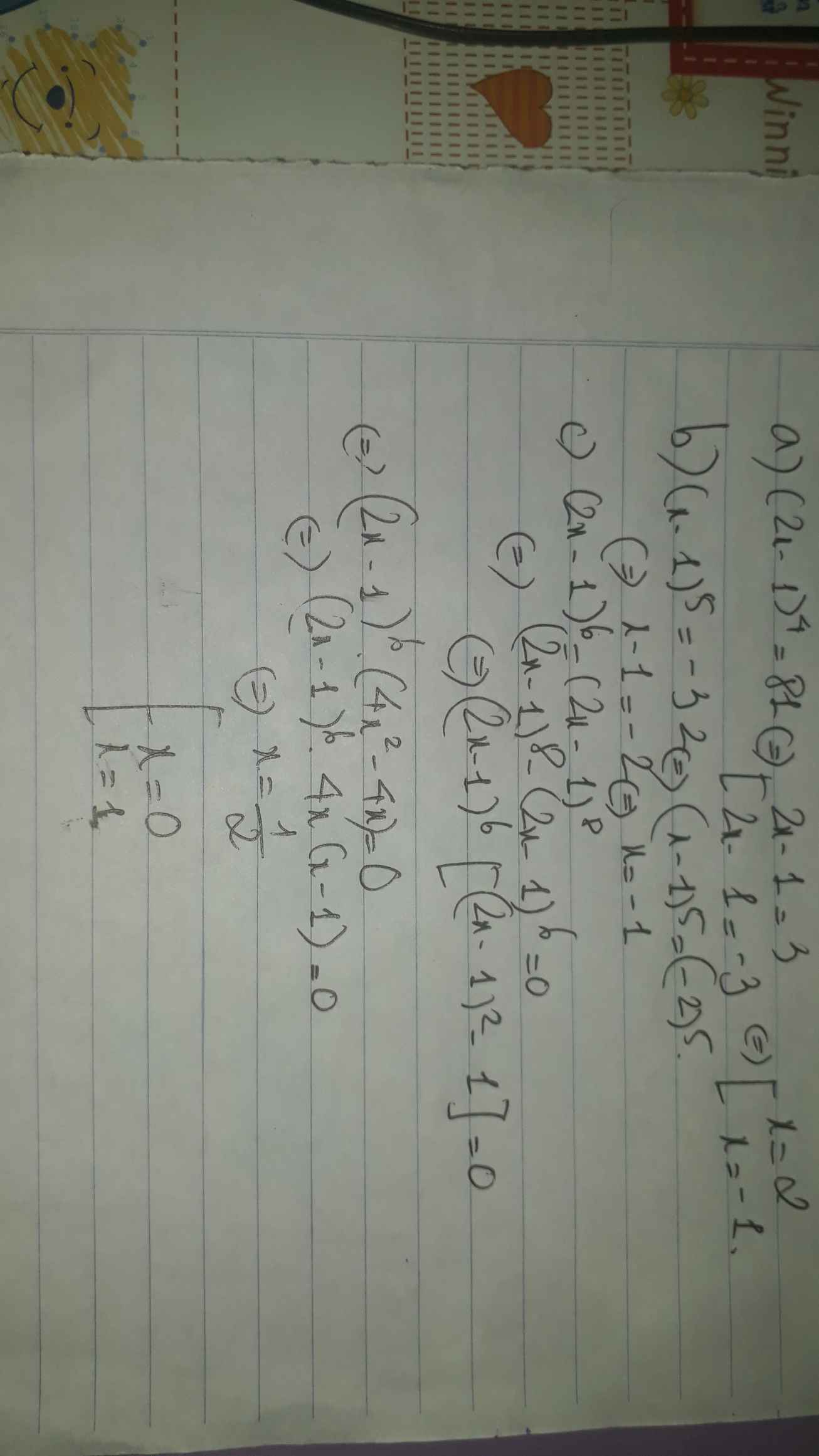
\(\left(2x+1\right)y-2x-1=-32\)
\(\Leftrightarrow2xy-2x+y-1=-32\)
\(\Leftrightarrow2x\left(y-1\right)+\left(y-1\right)=-32\)
\(\left(2x+1\right)\left(y-1\right)=-32\)
Đề bài nên cho là x,y thuộc Z; chia trường hợp rồi làm :vv
(2x + 1) y − 2x − 1 = −32
⇔2xy − 2x + y − 1 = −32
⇔2x (y − 1) + (y − 1) = −32
(2x + 1) (y − 1) = −32
=> 2x+1 và y-1 thuộc Ư(-32)
vậy.............................................................