NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
1
2 tháng 2 2021
Điều kiện: \(x\ge-1\)
PT \(\Rightarrow-2x-2\le x^2-2x-3\le2x+2\)
+) Xét \(x^2-2x-3\ge-2x-2\) \(\Leftrightarrow\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\)
+) Xét \(x^2-2x-3\le2x+2\) \(\Leftrightarrow\left[{}\begin{matrix}x\le-1\\x\ge5\end{matrix}\right.\)
\(\Rightarrow x\in(-\infty;-1]\cup[-5;+\infty)\)
PD
0
HP
16 tháng 2 2021
a, Phương trình có hai nghiệm trái dấu khi \(2\left(2m^2-3m-5\right)< 0\)
\(\Leftrightarrow\left(2m-5\right)\left(m+1\right)< 0\)
\(\Leftrightarrow-1< m< \dfrac{5}{2}\)
b, TH1: \(m^2-3m+2=0\Leftrightarrow\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\)
Phương trình đã cho có nghiệm duy nhất
TH2: \(m^2-3m+2\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m\ne2\end{matrix}\right.\)
Phương trình có hai nghiệm trái dấu khi \(-5\left(m^2-3m+2\right)< 0\)
\(\Leftrightarrow m^2-3m+2>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>2\\m< 1\end{matrix}\right.\)
Vậy \(m>2\) hoặc \(m< 1\)
HV
0
TD
1
9 tháng 11 2021
\(\Leftrightarrow\left|2x+4\right|-\left|1-x\right|=-3\)
AH
Akai Haruma
Giáo viên
3 tháng 8 2021
Lời giải:
ĐKXĐ: $x\neq 2$
PT $\Rightarrow x^2-1=x|x-2|$
Nếu $x>2$ thì pt trở thành: $x^2-1=x(x-2)=x^2-2x$
$\Leftrightarrow x=\frac{1}{2}< 2$ (loại)
Nếu $x< 2$ thì pt trở thành: $x^2-1=x(2-x)=2x-x^2$
$\Leftrightarrow 2x^2-2x-1=0$
$\Rightarrow x=\frac{1\pm \sqrt{3}}{2}$ (đều tm)
2 tháng 9 2017
Ta có :
\(\left|2x-1\right|=\left|2x+3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=2x+3\\2x-1=-2x-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-2x=3+1\\2x+2x=-3+1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}0=4\left(loại\right)\\4x=-2\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{-1}{2}\)
Vậy ...
PT
2 tháng 9 2017
\(\left|2x-1\right|=\left|2x+3\right|\)
\(\Rightarrow\left|2x-1\right|=2x+3\)
\(\Rightarrow2x-1=2x+3\) hoặc \(2x-1=-\left(2x+3\right)\)
\(\Rightarrow2x-2x=3+1\) hoặc \(2x-1=-2x-3\)
\(\Rightarrow0=4\) ( loại ) hoặc \(2x+2x=-3+1\)
\(\Rightarrow4x=-2\)
\(\Rightarrow x=\dfrac{-1}{2}\)
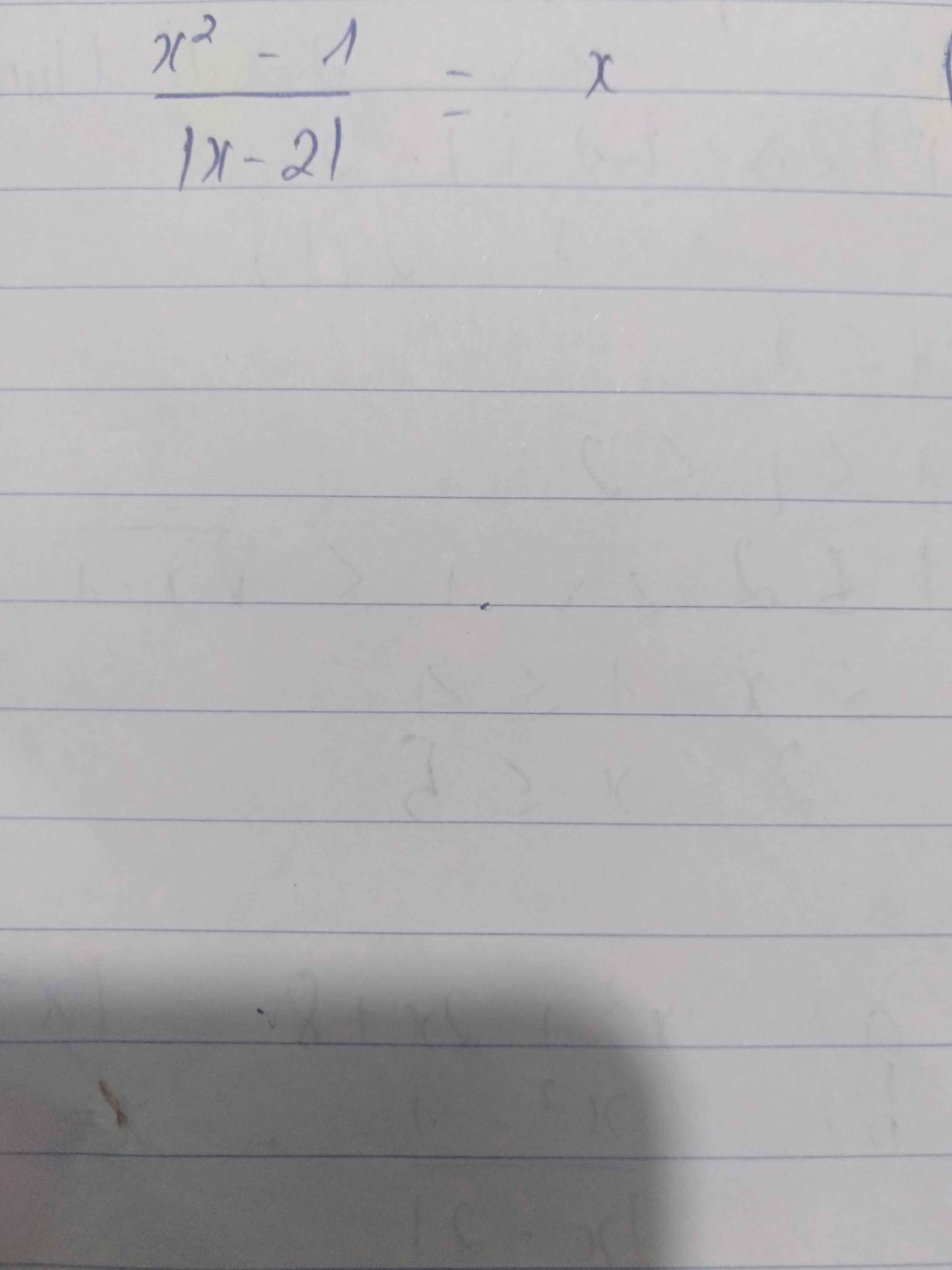
\(\left|2x+1\right|=5\)
\(\Rightarrow2x+1=\pm5\)
+) \(2x+1=5\Rightarrow2x=4\Rightarrow x=2\)
+) \(2x+1=-5\Rightarrow2x=-6\Rightarrow x=-3\)
Vậy \(x\in\left\{2;-3\right\}\)
\(\left|2x+1\right|=5\)
\(\Rightarrow\left[\begin{matrix}2x+1=5\\2x+1=-5\end{matrix}\right.\)
\(\Rightarrow\left[\begin{matrix}2x=5-1\\2x=-5-1\end{matrix}\right.\)
\(\Rightarrow\left[\begin{matrix}2x=4\\2x=-6\end{matrix}\right.\)
\(\Rightarrow\left[\begin{matrix}x=4:2\\x=-6:2\end{matrix}\right.\)
\(\Rightarrow\left[\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
Vậy : \(\left[\begin{matrix}x=2\\x=-3\end{matrix}\right.\)