
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Điều kiện: x> 0.
Lấy logarit cơ số của hai vế phương trình, ta được log5(x+3)= log2x
Do ![]() nên để phương trình có nghiệm thì x > 2
nên để phương trình có nghiệm thì x > 2
Lấy logarit cơ số của hai vế phương trình, ta được log5(x + 3) = log2x.
Đặt 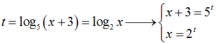
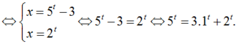
Chia hai vế phương trình cho 5t, ta được 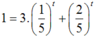 . Đây là phương trình hoành độ giao điểm của đường thẳng y = 1 (hàm hằng) và đồ thị hàm số
. Đây là phương trình hoành độ giao điểm của đường thẳng y = 1 (hàm hằng) và đồ thị hàm số 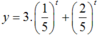 (hàm số này nghịch biến vì nó là tổng của hai hàm số nghịch biến).
(hàm số này nghịch biến vì nó là tổng của hai hàm số nghịch biến).
Do đó phương trình có nghiệm duy nhất. Nhận thấy t = 1 thỏa mãn phương trình. Với t = 1 thì x = 2 (thỏa mãn).
Vậy phương trình có nghiệm duy nhất.

Chọn B.
Điều kiện: x ≠ 0
Phương trình ![]()
Lấy logarit cơ số 3 hai vế của (*), ta được ![]()
![]()
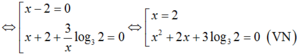
Vậy phương trình đã cho có nghiệm duy nhất x = 2.

Chọn B.
Điều kiện: 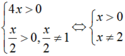
Phương trình 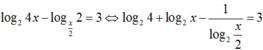
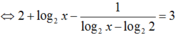
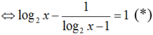
Đặt t = log2x với t ≠ 1, khi đó (*) 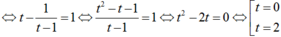
Với t = 0 , ta có log2x = 0 hay x = 1
Với t = 2, ta có log2x = 2 hay x = 4Vậy phương trình đã cho có hai nghiệm phân biệt.
23456 + 12345 = 35801 nha
/HT\
23456+12345= 35801 nhe
T I C K mik nha !
-HT-