K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 2 2016
Bài này có 2 cách giải, mình dùng định luật bảo toàn cho nhanh.
Chọn mốc thế năng ở chân mặt phẳng nghiêng.
Độ cao mặt phẳng nghiêng: \(h=10.\sin 30^0=5(m)\)
Ở đỉnh mặt phẳng nghiêng, cơ năng của vật: \(W_1=mgh\)
Ở chân mặt phẳng nghiêng, cơ năng là: \(W_2=\dfrac{1}{2}mv^2\)
Bảo toàn cơ năng: \(W_1=W_2\Rightarrow mgh=\dfrac{1}{2}mv^2\Rightarrow v=\sqrt{2gh}=\sqrt{2.10.5}=10(m/s)\)
26 tháng 3 2016
- Gọi: Khối lượng của ba chất lỏng trong ba bình là m(kg). Nhiệt dung riêng của chất lỏng ở bình 1, bình 2, bình 3 lần lượt là c1, c2, c3
- Nếu đổ 1/2 chất lỏng ở bình 1 vào bình 2 ta có phương trình
\(\frac{1}{2}\)m.c1.(t1- t12) = m.c2.(t12 - t2)
=> \(\frac{1}{2}\)mc1.(15-12) = m.c2.(12 - 10) => c2 = \(\frac{3}{4}\)c1 (1)
- Nếu đổ 1/2 chất lỏng ở bình 1 vào bình 3 ta có phương trình
\(\frac{1}{2}\)m.c1.(t1- t13) = m.c2.(t13 - t3)
=> \(\frac{1}{2}\)mc1.(19-15) = m.c3.(20 - 19) => 2c1 = c3 (2)
Đổ lẫn cả ba chất lỏng ở 3 bình vào nhau thì chất lỏng ở bình 2 thu nhiệt, chất lỏng ở bình 3 tỏa nhiệt. Không mất tính tổng quát nếu giả sử rằng bình 1 thu nhiệt vì dù bình 1 tỏa hay thu nhiệt thì PT cân bằng (3) dưới đây không thay đổi (*)
Chú ý: nếu không có lập luận (*) phải xét 2 trường hợp
Gọi t là nhiệt độ khi CB, Ta có phương trình cân bằng nhiệt:
m.c1.(t - t1) + m.c2.(t - t2) = m.c3.(t3 - t) (3)
Kết hợp (1) , (2) , ( 3 ) rồi rút gọn được
(t - 15) +\(\frac{3}{4}\)(t - 10) = 2(20 - t)
Tính được t = 16,67oC
V
violet
Giáo viên
14 tháng 4 2016
Khi sợi dây duỗi thẳng, có nghĩa các điểm trên dây ở VT cân bằng. Như vậy, giữa hai lần liên tiếp dây duỗi thẳng ứng với
thời gian từ đi từ VTCB ra biên rồi lại về VTCB, là T/2
Suy ra T/2 = 0,05s --> T = 0,1s
Theo đề bài: \(1,2=3.\dfrac{\lambda}{2}\Rightarrow \lambda = 0,8m\)
\(\Rightarrow v= \dfrac{\lambda}{T}=8(m/s)\)
15 tháng 4 2016
vậy cho e hỏi thêm trong mot buoc sóng thì biên độ của nó xác định như thế nào ạ
VT
7 tháng 8 2018
Đáp án A
Ta có:
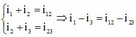
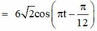(1)
Lại có
(2)
Từ (1) và (2)
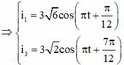
Dễ thấy i 1 vuông pha với i 3 , ta có:
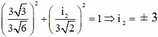mA
đang giảm nên
i
2
= -3 mA và đang ra biên âm.
0,23 A
0,23A