Y
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 5 2022
a: 3x+2>8
nên 3x>6
hay x>2
b: 4x-5<7
nên 4x<12
hay x<3
c: -2x+1<7
nên -2x<6
hay x>-3
d: -3x+13>-2
=>-3x>-15
hay x<5
DP
9 tháng 7 2017
a, \(1-\frac{2x-1}{9}=3-\frac{3x-3}{12}\)
\(\Leftrightarrow\frac{108-12\cdot\left(2x-1\right)}{108}=\frac{108\cdot3-9\cdot\left(3x-3\right)}{108}\)
\(\Rightarrow108-12\cdot\left(x-1\right)=108\cdot3-9\cdot\left(3x-3\right)\)
\(\Leftrightarrow108-24x+12=324-27x+27\)
\(\Leftrightarrow3x=231\)
\(\Rightarrow x=77\)
c,\(\frac{3}{4x-20}+\frac{15}{50-2x^2}+\frac{7}{6x+30}=0\)
\(\Rightarrow3\cdot\left(50-2x^2\right)\cdot\left(6x+30\right)+15\cdot\left(4x-20\right)\cdot\left(6x+30\right)+7\cdot\left(4x-20\right)\cdot\left(50-2x^2\right)=0\)
\(\Leftrightarrow900x+4500-36x^3-180x^2+360x^2+1800x-1800x-9000+1400x-56x^3-7000+280x^2=0\)
\(\Leftrightarrow-92x^3+460x^2+2300x-11500=0\)
\(\Leftrightarrow92x^3-460x^2-2300x+11500=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-5\\x=5\end{cases}}\)
28 tháng 5 2018
a) Thay x = 3 vào bất phương trình ta được: 2.3 + 3 < 9 <=> 9 < 9 (khẳng định sai)
Vậy x = 3 không là nghiệm của bất phương trình2x + 3 < 9
b) Thay x = 3 vào bất phương trình ta có: -4.3 > 2.3 + 5 => -12 > 11 (khẳng định sai)
Vậy x = 3 không là nghiệm của bất phương trình -4x > 2x + 5
c) Thay x = 3 vào bất phương trình ta có: 5 - 3 > 3.3 -12 => 2 > -3 (khẳng định đúng)
Vậy x = 3 là nghiệm của bất phương trình 5 - x > 3x - 12
21 tháng 3 2021
a)(2x+1)(3x-2)=(5x-8)(2x+1)
⇔(2x+1)(3x-2)-(5x-8)(2x+1)=0
⇔(2x+1)(3x-2-5x+8)=0
⇔(2x+1)(-2x+6)=0
⇔2x+1=0 hoặc -2x+6=0
1.2x+1=0⇔2x=-1⇔x=-1/2
2.-2x+6=0⇔-2x=-6⇔x=3
phương trình có 2 nghiệm x=-1/2 và x=3
TM
20 tháng 6 2017
b)\(3x^3+6x^2-75x-150=0\Leftrightarrow3\left(x^3+2x^2-25x-50\right)=0\Leftrightarrow x^3+2x^2-25x-50=0\)
<=>\(x^2\left(x+2\right)-25\left(x+2\right)=0\Leftrightarrow\left(x^2-25\right)\left(x+2\right)=0\Leftrightarrow\left(x-5\right)\left(x+5\right)\left(x+2\right)=0\)
<=>x-5=0 hoặc x+5=0 hoặc x+2=0<=>x=5 hoặc x=-5 hoặc x=-2
c)\(2x^5-3x^4+6x^3-8x^2+3=0\Leftrightarrow2x^5+x^4-4x^4-2x^3+8x^3+4x^2-12x^2+3=0\)
<=>\(x^4\left(2x+1\right)-2x^3\left(2x+1\right)+4x^2\left(2x+1\right)-3\left(4x^2-1\right)=0\)
<=>\(x^4\left(2x+1\right)-2x^3\left(2x+1\right)+4x^2\left(2x+1\right)-3\left(2x-1\right)\left(2x+1\right)=0\)
<=>\(\left(2x+1\right)\left(x^4-2x^3+4x^2-6x+3\right)=0\)
<=>\(\left(2x+1\right)\left(x^4-2x^3+x^2+3x^2-6x+3\right)=0\)
<=>\(\left(2x+1\right)\left[x^2\left(x^2-2x+1\right)+3\left(x^2-2x+1\right)\right]=0\)
<=>\(\left(2x+1\right)\left(x^2+3\right)\left(x^2-2x+1\right)=0\Leftrightarrow\left(2x+1\right)\left(x^2+3\right)\left(x-1\right)^2=0\)
Vì \(x^2\ge0\Rightarrow x^2+3\ge3>0\Rightarrow\orbr{\begin{cases}2x+1=0\\\left(x-1\right)^2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\x=1\end{cases}}\)
20 tháng 6 2017
a) 2x3 - x2 - 8x + 4 = 0
x2.(2x - 1) - 4.(2x - 1) = 0
(x2 - 4)(2x - 1) = 0
\(\Rightarrow\orbr{\begin{cases}x^2-4=0\\2x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x^2=4\\x=\frac{1}{2}\end{cases}}\)
Với x2 = 4
=> x = 2 hoặc x = -2
=> x = {-2 ; 2 ; \(\frac{1}{2}\))
22 tháng 2 2019
b) \(x^4+x^3-3x^2-4x-4=0\)
\(\Leftrightarrow x^4+2x^3-x^3-2x^2-x^2-2x-2x-4=0\)
\(\Leftrightarrow x^3\left(x+2\right)-x^2\left(x+2\right)-x\left(x+2\right)-2\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^3-x^2-x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^3-2x^2+x^2-2x+x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[x^2\left(x-2\right)+x\left(x-2\right)+\left(x-2\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-2\right)\left(x^2+x+1\right)=0\)
Vì \(x^2+x+1>0\forall x\)( cách c/m mình nói sau )
\(\Rightarrow\orbr{\begin{cases}x+2=0\\x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=2\end{cases}}}\)
Vậy....
22 tháng 2 2019
Cách chứng minh :
\(x^2+x+1\)
\(=x^2+2\cdot x\cdot\frac{1}{2}+\frac{1}{4}+\frac{3}{4}\)
\(=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x+\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\forall x\)
Hay \(x^2+x+1>0\forall x\)( đpcm )
TK
3 tháng 5 2019
a) Khai triển bình phương ròii giải như bình thường
b) <=>(x+2)(x2-2x+1)=0
sau đó tiếp tục giải phương trình tích là ra
c) <=>x (2x2-5x-7)=0
<=> x=0
hoặc 2x2-5x-7=0
bn đọc tự giải^^
#hoctốt
#plsss...k☺
2 tháng 4 2020
a) |x - 2| = 3
<=> \(\orbr{\begin{cases}x-2=3\\x-2=-3\end{cases}}\)
<=> \(\orbr{\begin{cases}x=5\\x=-1\end{cases}}\) Vậy S = {-1; 5}
b) \(\left|x+1\right|=\left|2x+3\right|\)
<=> \(\orbr{\begin{cases}x+1=2x+3\\x+1=-2x-3\end{cases}}\)
<=> \(\orbr{\begin{cases}-x=2\\3x=-4\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-2\\x=-\frac{4}{3}\end{cases}}\) Vậy S = {-2; -4/3}
c) \(\left|3x\right|=x+6\) (Đk: x \(\ge\)-6
<=> \(\orbr{\begin{cases}3x=x+6\\3x=-x-6\end{cases}}\)
<=> \(\orbr{\begin{cases}2x=6\\4x=-6\end{cases}}\)
<=> \(\orbr{\begin{cases}x=3\\x=-\frac{3}{2}\end{cases}}\)(tm)
Vậy S = {-3/2; 3}
2 tháng 4 2020
d) \(\left|x-5\right|=13-2x\)(Đk : x \(\le\)13/2)
<=> \(\orbr{\begin{cases}x-5=13-2x\\x-5=2x-13\end{cases}}\)
<=> \(\orbr{\begin{cases}3x=18\\-x=-8\end{cases}}\)
<=> \(\orbr{\begin{cases}x=6\\x=8\left(ktm\right)\end{cases}}\)Vậy S = {6}
e) |5x - 1| = x - 12 (Đk: x \(\ge\)12)
<=> \(\orbr{\begin{cases}5x-1=x-12\\5x-1=12-x\end{cases}}\)
<=> \(\orbr{\begin{cases}4x=-11\\6x=13\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-\frac{11}{4}\\x=\frac{13}{6}\end{cases}}\left(ktm\right)\)
=> pt vô nghiệm
f) \(\left|-2x\right|=3x+4\)(Đk: x \(\ge\)-4/3)
<=> \(\orbr{\begin{cases}-2x=3x+4\\2x=3x+4\end{cases}}\)
<=> \(\orbr{\begin{cases}-5x=4\\-x=4\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-\frac{4}{5}\\x=-4\left(ktm\right)\end{cases}}\) Vậy S = {-4/5}
S
25 tháng 4 2019
\(a,\Leftrightarrow\left(x+5\right)\left(x-3\right)=0\Leftrightarrow x\in\left\{-5;3\right\}\)
\(b,\Leftrightarrow\left(3x-1\right)\left(3x+1\right)=\left(3x+1\right)\left(4x+1\right)\)
\(\Leftrightarrow\orbr{\begin{cases}3x+1=0\\3x-1=4x+1\end{cases}}\)
\(c,\Leftrightarrow\left(2x^3-32x\right)+\left(3x^2-48\right)=0\Leftrightarrow2x\left(x-4\right)\left(x+4\right)+3\left(x-4\right)\left(x+4\right)\)
\(\Leftrightarrow\left(2x+3\right)\left(x+4\right)\left(x-4\right)=0\Leftrightarrow......\)
NN
21 tháng 5 2016
a) 10-4x=2x-2
<=>- 4x-2x = - 10 - 2
<=> -6x = - 12
<=> x= 2
Vậy PT có tập nghiệm x={ 12 }
b) \(\frac{5x-2}{3}\) = \(\frac{5-3x}{2}\)
<=> \(\frac{2\left(5x-2\right)}{6}\) = \(\frac{3\left(5-3x\right)}{6}\)
<=> \(\frac{10x-4}{6}\) = \(\frac{15-9x}{6}\)
=> 10x-4=15-9x
<=>10x+9x=4+15
<=>19x = 19
<=> x =1
Vậy PT có tập nghiệm x={1}
23 tháng 5 2016
c) 3x - 15 = 2x (x - 5)
= 3.(x-5)=2x(x-5)
Nếu x-5=0 => x=5 .Thỏa mãn 3.0=3.5.0.
Nếu x-5 khác 0 => 3=2x => x=3/2
Vậy PT có tập nghiệm là : x thuộc {0;3/2}
d) \(\frac{x^2-6}{x}=x+\frac{3}{2}=>\frac{x^2}{x}-\frac{6}{x}=x+\frac{3}{2}=>x-\frac{6}{x}=x+\frac{3}{2}\)
\(=>-\frac{6}{x}=\frac{3}{2}=>x=-4\)
Vây PT có tập nghiệm: x thuộc {-4}
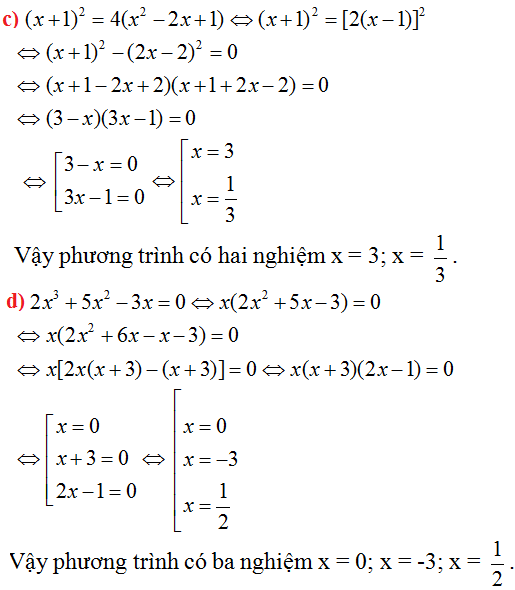
\(2|3-2x|-3x=13\)
* Nếu \(3-2x\ge0\Leftrightarrow2x\le3\Leftrightarrow x\le\frac{3}{2}\)
\(\Leftrightarrow|3-2x|=3-2x\)
\(2\left(3-2x\right)-3x=13\)
\(\Leftrightarrow6-4x-3x=13\)
\(\Leftrightarrow-7x-7=0\)
\(\Leftrightarrow x=-1\)( thỏa mãn )
* Nếu \(3-2x< 0\Leftrightarrow2x>3\Leftrightarrow x>\frac{3}{2}\)
\(\Leftrightarrow|3-2x|=-3+2x\)
\(2\left(-3+2x\right)-3x=13\)
\(\Leftrightarrow-6+4x-3x=13\)
\(\Leftrightarrow x=19\) ( thỏa mãn )
Vậy phương trình có tập nghiệm \(S=\left\{-1;19\right\}\)