Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\omega=2\pi=\pi;A=4cm\)
\(t=0:x_0;vo>0\)
=> 0 = cos φ => vo = -Aωsinϕ > 0
=> φ = +_pi/2 => sinω < 0
chọn φ = -π/2 => x = 4cos(2πt - π/2)cm.

Đáp án C
Phương pháp: Sử dụng lí thuyết đại cương về dao động điều hòa
Cách giải:
Biên độ: A = 5cm
Tần số góc: ω = π rad/s.
Tại t = 0, vật qua VTCB theo chiều dương: φ = - π/2 (rad)
=> x = 5cos(πt – π/2) cm

\(T=2s\)
Ta có: \(L=2A=8cm\Rightarrow A=4cm\)
Tần số góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{2}=\pi\)(rad/s)
Tại \(t=0\): \(\Rightarrow\left\{{}\begin{matrix}x=Acos\varphi=0\\v=-A\omega sin\varphi>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)\(\Rightarrow\varphi=-\dfrac{\pi}{2}\)
Phương trình dao động của vật:
\(x=4cos\left(\pi t-\dfrac{\pi}{2}\right)\)

Đáp án C
Phương pháp: Sử dụng lí thuyết về phương trình dao động̣ điều hoà
Cách giải :
Biên độ dao động : A = 8cm
Tần số góc:
![]()
Gốc thời gian làlúc vâṭqua VTCB theo chiều âm : φ = π 2
=>. Phương trình dao động: x = 8cos(10 π t + π/2) cm.

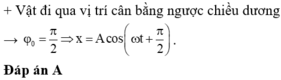

* Biên độ dao động A = 4cm
* Chu kì dao động T = 2s ⇒ ω = 2π/T = π rad/s
* Gốc thời gian là lúc vật qua vị trí cân bằng theo chiều dương
⇒ φ = - π/2 rad
Vậy phương trình dao động của vật là \(x\) = 4 cos ( πt - π/2 ) cm