
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta thấy : 12 \(⋮\)3, 15 \(⋮\)3, 21\(⋮\)3 do đó \(A\)\(⋮\)3 chỉ khi \(x\)\(⋮\)3.
Điều này nghĩa là x chia hết cho 3 .
Vậy x = 3k với k\(\in\)N .
Để \(A\)không chia hết cho 3 chỉ khi x không chia hết cho 3 .
Vậy nghĩa là x chia cho 3 có số dư khác 0 .
Vậy x = 3k + r với k,r \(\in\)N và 0 < r < 3 .
ta có A=12+15+21+x
A=48+x
để A chia hết cho 3 thì A=4+8+x chia hết cho 3
A=12+x chia hết cho 3
suy ra x thuộc {0;3;6;9}
để A ko chia hết cho 3 thì A ko thuộc {0;3;6;9}
k mink nhé

\(\begin{array}{l}21.0,1 - \left[ {4 - \left( { - 3,2 - 4,8} \right)} \right]:0,1\\ = 2,1 - \left[ {4 - \left( { - 8} \right)} \right]:0,1\\ = 2,1 - \left[ {4 + 8} \right]:0,1\\ = 2,1 - 12:0,1\\ = 2,1 - 12.10\\ = 2,1 - 120\\ = - \left( {120 - 2,1} \right)\\ = - 117,9\end{array}\)

C = (-1,7) . 2,3 + 1,7 . (-3,7) - 1,7 .3 - 0,17 : 0,1
=> C = -1,7 . 2,3 +( -1,7 ) . 3,7 - 1,7 . 3 - 1,7
=> C = -1,7 . ( 2,3 + 3,7 - 3 - 1 )
=> C = -1,7 . 2 = -3,4

\(\frac{a}{b}=\frac{21}{28}\)=> \(\frac{a}{b}=\frac{3}{4}\)=> \(\frac{a}{b}=\frac{3k}{4k}\)( \(k\inℤ,k\ne0\))
ƯCLN(a, b) = 15 => ƯCLN(3k, 4k) = 15
Mà ƯCLN(3k, 4k) = k
=> k = 15
=> a = 3 . 15 = 45
=> b = 4 . 15 = 60
=> \(\frac{a}{b}=\frac{45}{60}\)
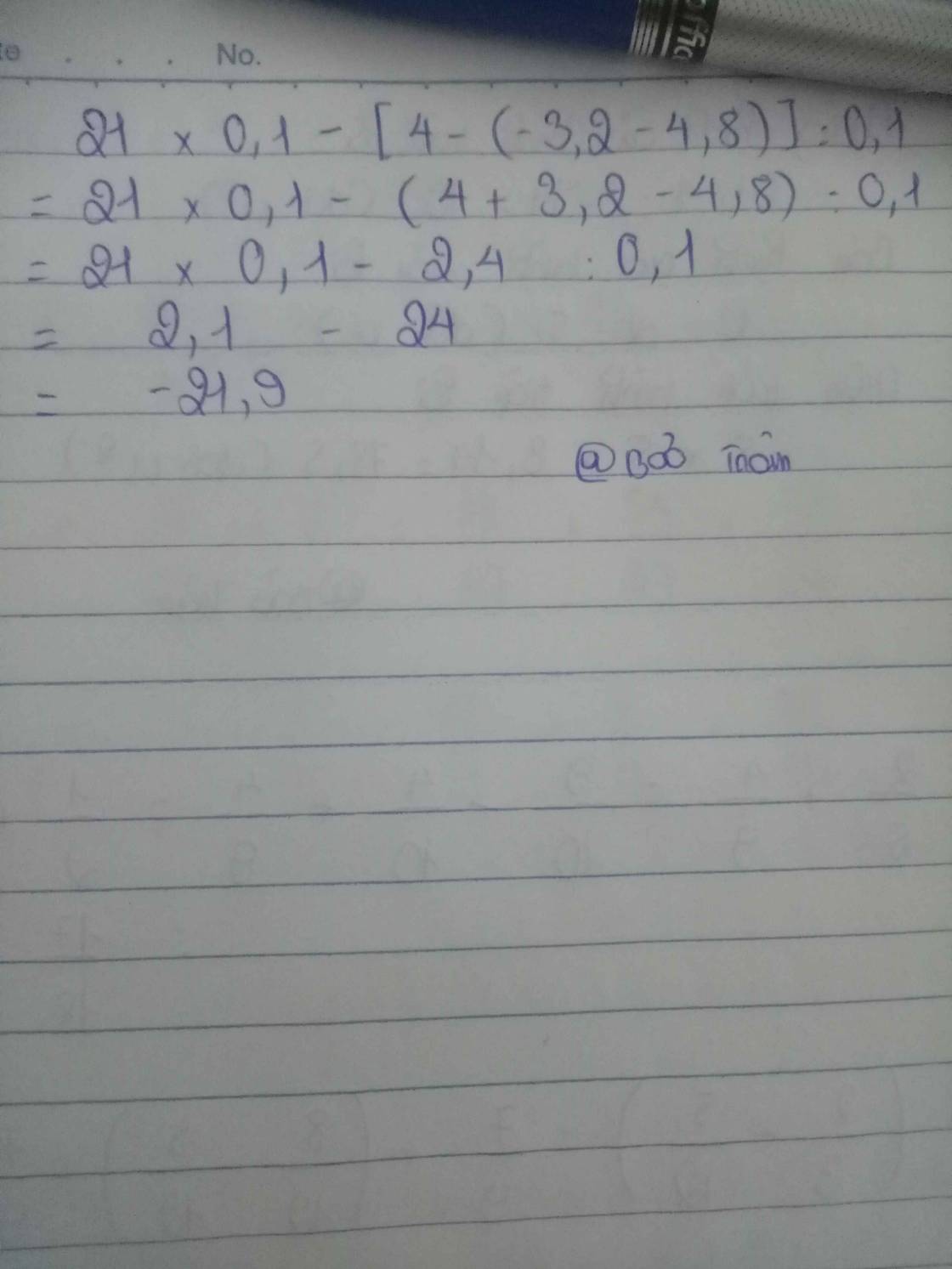
21. 0,1 [4 -(-3,2 - 4,8)] : 0,1
= 21. 0,1 [4 - (-8)] : 0,1
= 21.0,1. 12 : 0,1
= 2,1. 12 : 0,1
=252
\(21.0,1[ 4 - ( -3,2 - 4,8 )] : 0,1\)
\(= 2,1 . [ 4 - ( -8 )] . 10\)
\(= 2,1 . 10 . 12\)
\(= 21.12\)
\(= 252\)