K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 8 2023
`@` `\text {Ans}`
`\downarrow`
`(-2023) \times 33+2023 \times (-68)+2023`
`= 2023 \times (-33 - 68 + 1)`
`= 2023 \times (-101 + 1)`
`= 2023 \times (-100)`
`= -202300`
2 tháng 8 2023
-100 thì nhân với 2023 phải là -202300 mới đúng chứ ạ
2 tháng 8 2023
Có `xyz=2023=>2023=xyz`
Thay vào ta có :
\(\dfrac{xyz\cdot x}{xy+xyz\cdot x+xyz}+\dfrac{y}{yz+y+xyz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{x^2yz}{xy\left(1+xz+z\right)}+\dfrac{y}{y\left(z+1+xz\right)}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz}{1+xz+z}+\dfrac{1}{z+1+xz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz+1+z}{1+xz+z}=1\left(dpcm\right)\)
14 tháng 9 2023
Xét VT : x+3x+5x+7x+......+2023x
Số hạng của dãy số trên là : \(\dfrac{2023-1}{2}+1=1012\left(sốhạng\right)\)
Tổng số của dãy số trên là : \(\dfrac{\left(2023x+x\right).1012}{2}\text{=}1012x.1012\)
Do đó : ta có :
\(1012x.1012\text{=}2023.2024\)
\(1012x\text{=}4046\)
\(x\text{=}\dfrac{2023}{506}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 9 2023
VT = x + 3x + 5x + 7x +... + 2023x = [(2023 - 1):2 +1] . (2023+1)x = 1012. 2024x = 2048288x
VP= 2023 . 2024= 4094552
VT=VP <=> 2048288x =4094552
<=>\(x\approx2\)
OK
4
13 tháng 12 2023
a)(−2023).33+2023.(−68)+2023�)(-2023).33+2023.(-68)+2023
=2023.(−33−68+1)=2023.(-33-68+1)
=2023.(−100)=2023.(-100)
=−202300=-202300
b)(38−29+43)−(43+38)�)(38-29+43)-(43+38)
=38−29+43−43−38=38-29+43-43-38
=(38−38)−29+(43−43)=(38-38)-29+(43-43)
=−29=-29
=−29=-29
ND
1
HK
Cho \(A=\dfrac{2023^{30}+5}{2023^{31}+5}\) và \(B=\dfrac{2023^{31}+5}{2023^{32}+5}\). So sánh A và B
2
17 tháng 4 2023
Áp dụng tính chất : Nếu \(\dfrac{a}{b}< 1\) thì \(\dfrac{a}{b}< \dfrac{a+n}{b+n}\) ( a; b; n ϵ N , b; n ≠ 0 )
Ta có \(\dfrac{2023^{31}+5}{2023^{32}+5}< 1\)
⇒ \(B=\dfrac{2023^{31}+5}{2023^{32}+5}< \dfrac{2023^{31}+5+2018}{2023^{32}+5+2018}=\dfrac{2023^{31}+2023}{2023^{32}+2023}=\dfrac{2023\left(2023^{30}+1\right)}{2023\left(2023^{31}+1\right)}=\dfrac{2023^{30}+1}{2023^{31}+1}=A\)Vậy A > B
XO
17 tháng 4 2023
Ta có 2023A = \(\dfrac{2023.\left(2023^{30}+5\right)}{2023^{31}+5}=\dfrac{2023^{31}+5.2023}{2023^{31}+5}\)
\(=1+\dfrac{2022.5}{2023^{31}+5}\)
Lại có 2023B = \(\dfrac{2023.\left(2023^{31}+5\right)}{2023^{32}+5}=\dfrac{2023^{32}+2023.5}{2023^{32}+5}\)
\(=1+\dfrac{2022.5}{2023^{32}+5}\)
Dễ thấy 202331 + 5 < 202332 + 5
\(\Leftrightarrow\dfrac{2022.5}{2023^{31}+5}>\dfrac{2022.5}{2023^{32}+5}\)
\(\Leftrightarrow1+\dfrac{2022.5}{2023^{31}+5}>1+\dfrac{2022.5}{2023^{32}>5}\)
\(\Leftrightarrow2023A>2023B\Leftrightarrow A>B\)
TL
1
23 tháng 2 2023
\(2023A=\dfrac{2023^{31}+4046}{2023^{31}+2}=1+\dfrac{4044}{2023^{31}+2}\)
\(2023B=\dfrac{2023^{32}+4046}{2023^{32}+2}=1+\dfrac{4044}{2023^{32}+2}\)
mà 2023^31+2<2023^32+2
nên A>B
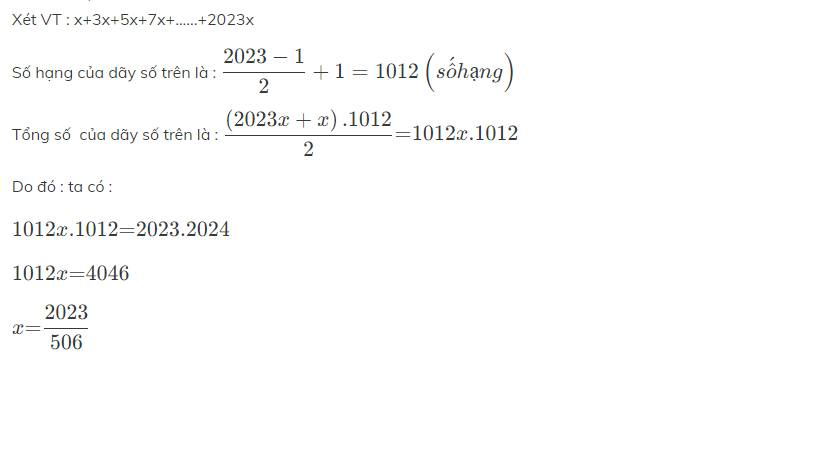
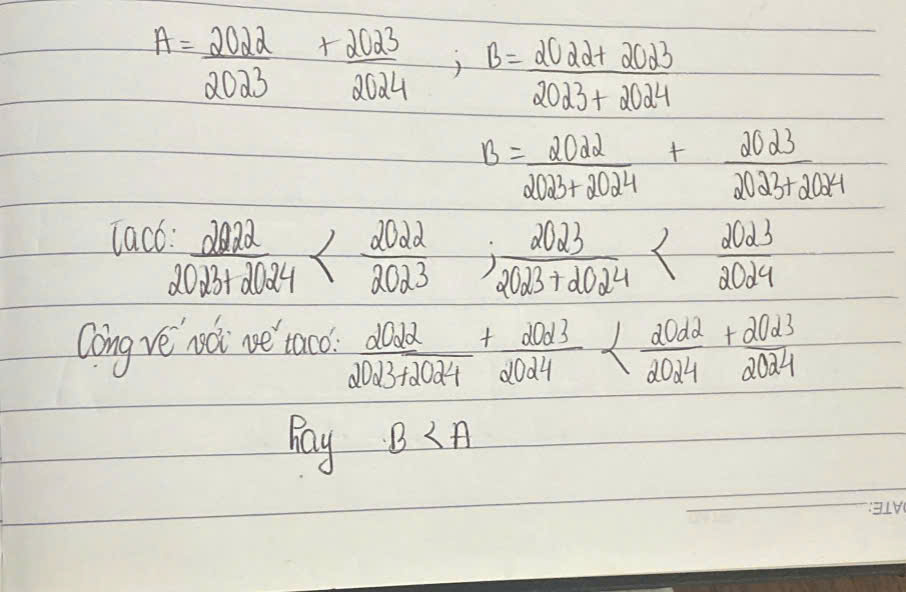
Tính nhanh được thì em cảm ơn
Bạn nãy vừa đăng câu này rồi mà, bạn chú ý phần thông báo để nhận lời giải nha.